
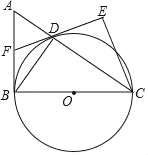
【题目】如图,已知直角△ABC中,∠ABC=90°,BC为圆O的直径,D为圆O与斜边AC的交点,DE为圆O的切线,DE交AB于F,且CE⊥DE.
(1)求证:CA平分∠ECB;
(2)若DE=3,CE=4,求AB的长;
(3)记△BCD的面积为S1,△CDE的面积为S2,若S1:S2=3:2.求sin∠AFD的值.
【答案】(1)详见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1),连接OD,由DE是⊙O的切线可知OD⊥DE,由CE⊥DE,可知OD∥CE,进而可知∠ECD=∠CDO,因为∠CDO=∠DCO,所以∠ECD=∠DCO,即可证明.(2)连接BD,根据勾股定理可求出CD=5,所以tan∠ECD=![]() =
=![]() ,在根据各直角三角形中各边的函数关系即可求出AB的长.(3)过点D作DG⊥BC于G,由CA∠BCE,可知DG=DE,进而△CDG≌△CDE根据S1:S2=3:2得
,在根据各直角三角形中各边的函数关系即可求出AB的长.(3)过点D作DG⊥BC于G,由CA∠BCE,可知DG=DE,进而△CDG≌△CDE根据S1:S2=3:2得![]() ,得
,得![]() ,所以BC=3BG,OD=OC=
,所以BC=3BG,OD=OC=![]() BC=
BC=![]() BG,根据勾股定理可求出DG得长,进而可求出sin∠DOG的值,根据四边形内角和可知∠AFD=∠DOG,即可求出sin∠AFD的值.
BG,根据勾股定理可求出DG得长,进而可求出sin∠DOG的值,根据四边形内角和可知∠AFD=∠DOG,即可求出sin∠AFD的值.
(1)如图,连接OD,
∵DE是⊙O的切线,
∴OD⊥DE,
∵CE⊥DE,
∴OD∥CE,
∴∠ECD=∠CDO,
∵∠CDO=∠DCO,
∴∠ECD=∠DCO,
∴CA平分∠ECB;
(2)如图,连接BD,∵BD为直径,
∴∠BDC=90°,
在Rt△CED中,DE=3,CE=4,根据勾股定理得,DC=5,
∴tan∠ECD=![]() =
=![]() ,
,
∴BD=DCtan∠DCB=![]() ,
,
∵∠BCD+∠CBD=90°,∠ABD+∠CBD=90°,![]()
∴∠BCD=∠ABD,
在Rt△CDE中,cos∠DCE=![]() =
=![]() ,
,
∴cos∠BCD=![]() ,
,
∴cos∠ABD=![]() ,
,
在Rt△ABD中,cos∠ABD=![]() =
=![]() ,
,
∴AB=![]() ×
×![]() =
=![]() ;
;
(3)如图,
过点D作DG⊥BC于G,
∵CA平分∠BCE,
∴DG=DE,
易知,△CDG≌△CDE,
∴S2=S△CDG=S△CDE,
∵S1:S2=3:2,
∴![]() ,
,
∴,![]()
∴![]() ,
,
设BG=x,则CG=2x,
∴BC=BG+CG=3x,
∴OD=OC=![]() BC=
BC=![]() x,
x,
∴OG=CG﹣OC=2x﹣![]() x=
x=![]() x,
x,
在Rt△ODG中,根据勾股定理得,DG=![]() x,sin∠DOG=
x,sin∠DOG=![]() =
=![]() =
=![]() ,
,
在四边形OBFD中,根据四边形内角和得,∠BFD+∠DOG=180°,
∵∠AFD+∠BFD=180°,
∴∠AFD=∠DOG,
∴sin∠AFD=![]() .
.


科目:初中数学 来源: 题型:
【题目】两个一次函数l1、l2的图象如图:

(1)分別求出l1、l2两条直线的函数关系式;
(2)求出两直线与y轴围成的△ABP的面积;
(3)观察图象:请直接写出当x满足什么条件时,l1的图象在l2的下方.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,点D、E分别在AB、AC上,且BD=CE.
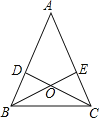
(1)找出图中所有的全等的三角形.
(2)选一组全等三角形进行证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(0<2a<b)的顶点为P(x0,y0),点A(1,yA),B(0,yB),C(﹣1,yC)在该抛物线上,当y0≥0恒成立时,![]() 的最小值为( )
的最小值为( )
A. 1 B. 2 C. 4 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,有一条线段AB,已知点A(﹣3,0)和B(0,4),平移线段AB得到线段A1B1.若点A的对应点A1的坐标为(0,﹣1),则线段AB平移经过的区域(四边形ABB1A1)的面积为( )
A. 12 B. 15 C. 24 D. 30
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中的每个小正方形边长都是1.请同学们利用网格线进行画图:
(1)在图1中,画一个顶点为格点、面积为5的正方形;
(2)在图2中,已知线段AB、CD,画线段EF,使它与AB、CD组成轴对称图形;(要求画出所有符合题意的线段)
(3)在图3中,找一格点D,满足:①到CB、CA的距离相等;②到点A、C的距离相等.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com