
【题目】有一个面积为1的正方形,经过一次“生长”后,在他的左右肩上生出两个小正方形,其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,变成了下图,如果继续“生长”下去,它将变得“枝繁叶茂”,请你算出“生长”了2019次后形成的图形中所有的正方形的面积和是( )

A.1B.2018C.2019D.2020
【答案】D
【解析】
根据勾股定理和正方形的面积公式,知“生长”1次后,以直角三角形两条直角边为边长的正方形的面积和等于以斜边为边长的正方形的面积,即所有正方形的面积和是2×1=2;“生长”2次后,所有的正方形的面积和是3×1=3,推而广之即可求出“生长”2019次后形成图形中所有正方形的面积之和.
解:设直角三角形的是三条边分别是a,b,c.
根据勾股定理,得a2+b2=c2,
即正方形A的面积+正方形B的面积=正方形C的面积=1.
正方形D的面积+正方形E的面积+正方形F的面积+正方形G的面积=正方形A的面积+正方形B的面积=正方形C的面积=1.
推而广之,即:每次“生长”的正方形面积和为1,“生长”了2019次后形成的图形中所有的正方形的面积和是2020×1=2020.
故选:D.


科目:初中数学 来源: 题型:
【题目】某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利44元,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出5件。若商场平均每天要盈利1600元,每件衬衫应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,以BC为半径作⊙B,交AB于点C,交AB的延长线于点E,连接CD、CE.

(1)求证:△ACD∽△AEC;
(2)当![]() 时,求tanE;
时,求tanE;
(3)若AD=4,AC=4![]() ,求△ACE的面积.
,求△ACE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:已知,如图(1),在面积为S的△ABC中, BC=a,AC=b, AB=c,内切圆O的半径为r连接OA、OB、OC,△ABC被划分为三个小三角形.
![]()
∴![]() .
.

(1)类比推理:若面积为S的四边形ABCD存在内切圆(与各边都相切的圆),如图(2),各边长分别为AB=a,BC=b,CD=c,AD=d,求四边形的内切圆半径r;
(2)理解应用:如图(3),在等腰梯形ABCD中,AB∥DC,AB=21,CD=11,AD=13,⊙O1与⊙O2分别为△ABD与△BCD的内切圆,设它们的半径分别为r1和r2,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后都停留一段时间,然后分别按原速一同驶往甲地后停车.设慢车行驶的时间为x小时,两车之间的距离为y千米,图中折线表示y与x之间的函数图象,请根据图象解决下列问题:
(1)甲乙两地之间的距离为 千米;
(2)求快车和慢车的速度;
(3)求线段DE所表示的y与x之间的函数关系式,并写出自变量x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李从如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,观察得出了下面四条信息:①b2﹣4ac>0;②c>1;③ab>0;④a﹣b+c<0.你认为其中正确的有( ).

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知x1=3是关于x的一元二次方程x2-4x+c=0的一个根,求c的值和方程的另一个根.
(2)如图,在矩形ABCD中.点O在边AB上,∠AOC=∠BOD.求证:AO=OB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)某校在基地参加社会实践话动中,带队老师考问学生:基地计划新建一个矩形的生物园地,一边靠旧墙(墙足够长),另外三边用总长69米的不锈钢栅栏围成,与墙平行的一边留一个宽为3米的出入口,如图所示,如何设计才能使园地的而积最大?下面是两位学生争议的情境:
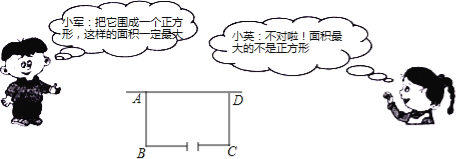
请根据上面的信息,解决问题:
(1)设AB=x米(x>0),试用含x的代数式表示BC的长;
(2)请你判断谁的说法正确,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 轴于点
轴于点![]() ,直线
,直线![]() 轴于点
轴于点![]() ,直线
,直线![]() 轴于点
轴于点![]() ,…直线
,…直线![]() 轴于点
轴于点![]() .函数
.函数![]() 的图像与直线
的图像与直线![]() 分别变于点
分别变于点![]() ;函数
;函数![]() 的图像与直线
的图像与直线![]() 分别交于点
分别交于点![]() ,如果
,如果![]() 的面积记的作
的面积记的作![]() ,四边形
,四边形![]() 的面积记作
的面积记作![]() ,四边形
,四边形![]() 的面积记作
的面积记作![]() ,…四边形
,…四边形![]() 的面积记作
的面积记作![]() ,那么
,那么![]() ________.
________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com