
【题目】如图,在Rt△ABC中,∠ACB=90°,以BC为半径作⊙B,交AB于点C,交AB的延长线于点E,连接CD、CE.

(1)求证:△ACD∽△AEC;
(2)当![]() 时,求tanE;
时,求tanE;
(3)若AD=4,AC=4![]() ,求△ACE的面积.
,求△ACE的面积.
【答案】(1)证明见解析(2)![]() (3)12
(3)12![]()
【解析】试题分析:(1)、根据直径所对的圆周角为直角以及BC=CE得出∠ACD=∠E,然后根据∠A为公共角得出三角形相似;(2)、设AC=4k,则BC=3k,则AE=8k,根据三角形相似得出tanE=![]() =
=![]() 得出答案;(3)、过点E作EH⊥AC,垂足为H.设⊙B的半径为R,根据Rt△ABC的勾股定理得出R的值,然后根据△ABC∽△AEH得出EH的长度,从而求出△ACE的面积.
得出答案;(3)、过点E作EH⊥AC,垂足为H.设⊙B的半径为R,根据Rt△ABC的勾股定理得出R的值,然后根据△ABC∽△AEH得出EH的长度,从而求出△ACE的面积.
试题解析:(1)∵DE为⊙B的直径,
∴∠DCE=90°,
∵∠ACB=90°,∠ACD=∠BCE.
∵BC=CE,
∴∠BCE=∠E,
∴∠ACD=∠E,
又∵∠CAD=∠EAC,
∴△ACD∽△AEC;
(2)∵![]() ,
,
设AC=4k,则BC=3k,
∴在Rt△ABC中,AB=5k,BD=3k,AE=AB+BE=8k.
由(1)知:△DCE为直角三角形,
则tanE=![]() .
.
∵△ACD∽△AEC,
∴![]() =
=![]() =
=![]() =
=![]() ,
,
即tanE=![]() =
=![]() ;
;
(3)过点E作EH⊥AC,垂足为H.设⊙B的半径为R.
∵在Rt△ABC中,∠ACB=90°,
∴AB2=AC2+BC2,
∴(4+R)2=(4![]() )2+R2,
)2+R2,
解得R=4.
即BC=4,DE=2BC=8,AB=8,AE=12.
∵∠ACB=∠AHE=90°,∠CAB=∠CAE,
∴△ABC∽△AEH,
∴![]() ,
,
即![]() ,
,
解得EH=6,
∴△ACE的面积为![]() AC·EH=
AC·EH=![]() ×4
×4![]() ×6=12
×6=12![]()


科目:初中数学 来源: 题型:
【题目】如图,边长分别为2和4的两个等边三角形,开始它们在左边重叠,大△ABC固定不动,然后把小△A′B′C′自左向右平移,直至移到点B′到C重合时停止.设小三角形移动的距离为x,两个三角形的重合部分的面积为y,则y关于x的函数图象是( )
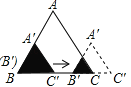
A. 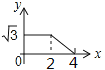 B.
B. 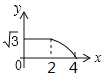 C.
C. 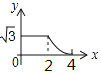 D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲,乙,丙三人各有邮票若干枚,要求互相赠送.先由甲送给乙,丙,所给的枚数等于乙,丙原来各有的邮票数;然后依同样的游戏规则再由乙送给甲,丙现有的邮票数,最后由丙送给甲,乙现有的邮票数.互相送完后,每人恰好各有64枚.你能知道他们原来各有邮票多少枚吗?说出你的思考过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABD和△ACE中,有下列四个等式:①AB=AC;②AD=AE;③∠1=∠2;④BD=CE.以其中三个条件为题设,填入已知栏中,一个论断为结论,填入下面求证栏中,使之组成一个真命题,并写出证明过程.

已知: .
求证: .
证明:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】组装甲、乙、丙3种产品,需用A、B、C3种零件.每件甲需用A、B各2个;每件乙需用B、C各1个;每件丙需用2个A和1个C.用库存的A、B、C3种零件,如组装成p件甲产品、q件乙产品、r件丙产品,则剩下2个A和1个B,C恰好用完.求证:无论怎样改变生产甲、乙、丙的件数,也不能把库存的A、B、C3种零件都恰好用完.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com