
分析 (1)根据平均单价=$\frac{总钱数}{两次购买的斤数和}$求出甲、乙所购饲料的平均单价即可;
(2)根据作差法比较两单价的大小即可.
解答 解:(1)∵两次购买的饲料单价分别为m元/千克和n元/千克(m,n是正数,且m≠n),
∴甲两次购买饲料的平均单价为$\frac{1000m+1000n}{2×1000}$=$\frac{m+n}{2}$(元/千克),
乙两次购买饲料的平均单价为$\frac{800×2}{\frac{800}{m}+\frac{800}{n}}$=$\frac{2mn}{m+n}$(元/千克);
(2)甲、乙两种饲料的平均单价的差是:
$\frac{m+n}{2}$-$\frac{2mn}{m+n}$=$\frac{(m+n)^{2}}{2(m+n)}$-$\frac{4mn}{2(m+n)}$=$\frac{{m}^{2}+2mn+{n}^{2}-4mn}{2(m+n)}$=$\frac{{(m-n)}^{2}}{2(m+n)}$,
由于m、n是正数,因为m≠n时,$\frac{(m-n)^{2}}{2(m+n)}$也是正数,
即$\frac{m+n}{2}$-$\frac{2mn}{m+n}$>0,
因此乙的购货方式更合算.
点评 本题考查的是分式的混合运算,熟知分式混合运算的法则是解答此题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA边上的中点,阅读下列材料,回答问题:
在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA边上的中点,阅读下列材料,回答问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
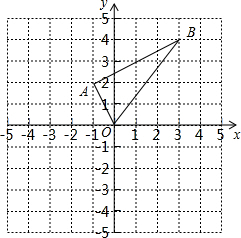 如图在平面直角坐标系中,已知点A(-1,2),B(3,4).
如图在平面直角坐标系中,已知点A(-1,2),B(3,4).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com