练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图是由4个大小相等的正方形搭成的几何体，其左视图是（　　）

    　

    A．

    B．

    C．

    D．

     


    C

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    任意大于1的正整数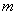的三次幂均可“分裂”成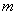个连续奇数的和，如：，

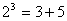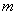    ，,按此规律，若分裂后其中有一个奇数是2015，则的值是（  ）

    A. 46          B. 45          C.44          D. 43

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，已知AB是⊙O的直径，点P在BA的延长线上，PD切⊙O于点D，过点B作BE垂直于PD，交PD的延长线于点C，连接AD并延长，交BE于点E．

    （1）求证：AB=BE；

    （2）若PA=2，cosB=，求⊙O半径的长．

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，已知抛物线y=ax2+bx+c与x轴交于A、B两点，顶点C的纵坐标为﹣2，现将抛物线向右平移2个单位，得到抛物线y=a1x2+b1x+c1，则下列结论正确的是　　．（写出所有正确结论的序号）

    ①b＞0

    ②a﹣b+c＜0

    ③阴影部分的面积为4

    ④若c=﹣1，则b2=4a．

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


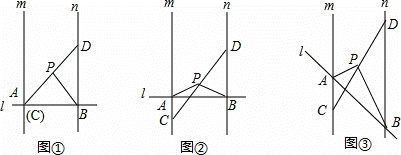
    已知直线m∥n，点C是直线m上一点，点D是直线n上一点，CD与直线m、n不垂直，点P为线段CD的中点．

    （1）操作发现：直线l⊥m，l⊥n，垂足分别为A、B，当点A与点C重合时（如图①所示），连接PB，请直接写出线段PA与PB的数量关系：　PA=PB　．

    （2）猜想证明：在图①的情况下，把直线l向上平移到如图②的位置，试问（1）中的PA与PB的关系式是否仍然成立？若成立，请证明；若不成立，请说明理由．

    （3）延伸探究：在图②的情况下，把直线l绕点A旋转，使得∠APB=90°（如图③所示），若两平行线m、n之间的距离为2k．求证：PA•PB=k•AB．

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，已知AB=AC=AD，∠CBD=2∠BDC，∠BAC=44°，则∠CAD的度数为（　　）

    　

    A．

    68°

    B．

    88°

    C．

    90°

    D．

    112°

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    分式方程的解为　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    比较大小：4　　（填“＞”或“＜”）

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    复数（为虚数单位），为的共轭复数，则下列结论正确的是

    A. 的实部为    B. 的虚部为    C.    D.

    查看答案和解析>>

    同步练习册答案