
【题目】如图1,在正方形ABCD中,E、F分别为BC、CD的中点,连接AE、BF,交点为G.
(1)求证:AE⊥BF;
(2)将△BCF沿BF对折,得到△BPF(如图2),延长FP到BA的延长线于点Q,求sin∠BQP的值;
(3)将△ABE绕点A逆时针方向旋转,使边AB正好落在AE上,得到△AHM(如图3),若AM和BF相交于点N,当正方形ABCD的面积为4时,求四边形GHMN的面积.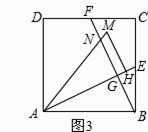
【答案】
(1)
证明:如图1,
∵E,F分别是正方形ABCD边BC,CD的中点,
∴CF=BE,
在Rt△ABE和Rt△BCF中,

∴Rt△ABE≌Rt△BCF(SAS),
∠BAE=∠CBF,
又∵∠BAE+∠BEA=90°,
∴∠CBF+∠BEA=90°,
∴∠BGE=90°,
∴AE⊥BF.
(2)
解:如图2,根据题意得,
FP=FC,∠PFB=∠BFC,∠FPB=90°
∵CD∥AB,
∴∠CFB=∠ABF,
∴∠ABF=∠PFB,
∴QF=QB,
令PF=k(k>0),则PB=2k
在Rt△BPQ中,设QB=x,
∴x2=(x﹣k)2+4k2,
∴x= ![]() ,
,
∴sin∠BQP= ![]() =
= ![]() =
= ![]() .
.
(3)
解:∵正方形ABCD的面积为4,
∴边长为2,
∵∠BAE=∠EAM,AE⊥BF,
∴AN=AB=2,
∵∠AHM=90°,
∴GN∥HM,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴S△AGN= ![]() ,
,
∴S四边形GHMN=S△AHM﹣S△AGN=1﹣ ![]() =
= ![]() ,
,
∴四边形GHMN的面积是 ![]() .
.
【解析】(1)运用Rt△ABE≌Rt△BCF,再利用角的关系求得∠BGE=90°求证;(2)△BCF沿BF对折,得到△BPF,利用角的关系求出QF=QB,解出BP,QB求解;(3)先求出正方形的边长,再根据面积比等于相似边长比的平方,求得S△AGN= ![]() ,
,
再利用S四边形GHMN=S△AHM﹣S△AGN求解.


 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,顶点为(3,4)的抛物线交y轴于A点,交x轴于B、C两点(点B在点C的左侧),已知A点坐标为(0,﹣5).
(1)求此抛物线的解析式;
(2)过点B作线段AB的垂线交抛物线于点D,如果以点C为圆心的圆与直线BD相切,请判断抛物线的对称轴l与⊙C有什么位置关系,并给出证明;
(3)在抛物线上是否存在一点P,使△ACP是以AC为直角边的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,该小组发现8米高旗杆DE的影子EF落在了包含一圆弧型小桥在内的路上,于是他们开展了测算小桥所在圆的半径的活动.小刚身高1.6米,测得其影长为2.4米,同时测得EG的长为3米,HF的长为1米,测得拱高(弧GH的中点到弦GH的距离,即MN的长)为2米,求小桥所在圆的半径. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,弦AB与弦CD相交于点G,OA⊥CD于点E,过点B的直线与CD的延长线交于点F,AC∥BF. 
(1)若∠FGB=∠FBG,求证:BF是⊙O的切线;
(2)若tan∠F= ![]() ,CD=a,请用a表示⊙O的半径;
,CD=a,请用a表示⊙O的半径;
(3)求证:GF2﹣GB2=DFGF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CB=CA,∠ACB=90°,点D在边BC上(与B、C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论: ①AC=FG;②S△FAB:S四边形CBFG=1:2;③∠ABC=∠ABF;④AD2=FQAC,
其中正确的结论的个数是 . 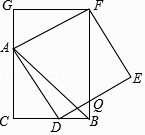
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为1的正方形ABCD的对角线AC、BD相交于点O,有直角∠MPN,使直角顶点P与点O重合,直角边PM、PN分别与OA、OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<90°),PM、PN分别交AB、BC于E、F两点,连接EF交OB于点G,则下列结论中正确的是 .
①EF= ![]() OE;②S四边形OEBF:S正方形ABCD=1:4;③BE+BF=
OE;②S四边形OEBF:S正方形ABCD=1:4;③BE+BF= ![]() OA;④在旋转过程中,当△BEF与△COF的面积之和最大时,AE=
OA;④在旋转过程中,当△BEF与△COF的面积之和最大时,AE= ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC 是等边三角形,点P 是三角形内的任意一点,PD∥AB,PE∥BC,PF∥AC,若△ABC 的周长为36,则PD+PE+PF=( )
A.12
B.8
C.4
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB为⊙O的直径,BC⊥AB于B,且BC=AB,D为半圆⊙O上的一点,连接BD并延长交半圆⊙O的切线AE于E.
(1)如图1,若CD=CB,求证:CD是⊙O的切线;
(2)如图2,若F点在OB上,且CD⊥DF,求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小苏和小林在如图1所示的跑道上进行4×50米折返跑.在整个过程中,跑步者距起跑线的距离y(单位:m)与跑步时间t(单位:s)的对应关系如图2所示.下列叙述正确的是( ) 
A.两人从起跑线同时出发,同时到达终点
B.小苏跑全程的平均速度大于小林跑全程的平均速度
C.小苏前15s跑过的路程大于小林前15s跑过的路程
D.小林在跑最后100m的过程中,与小苏相遇2次
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com