练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    点A关于x轴对称的点的坐标为（m，-3），关于y轴对称的点的坐标（2，n），那么点A的坐标是（　　）
    A、（m，-n）
    B、（-m，n）
    C、（-3，2）
    D、（-2，3）
    考点：关于x轴、y轴对称的点的坐标
    专题：
    分析：分别利用关于x轴对称以及关于y轴对称点的性质表示出A点坐标，即可得出m，n的值，进而得出答案．
    解答：解：∵点A关于x轴对称的点的坐标为（m，-3），
    ∴A（m，3），
    ∵A点关于y轴对称的点的坐标为（2，n），
    ∴A（-2，n），
    ∴m=-2，n=3，
    ∴A（-2，3）．
    故选：D．
    点评：此题主要考查了关于x轴、y轴对称点的性质，正确把握横纵坐标的关系是解题关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    如图：在平面直角坐标系中，A（-2，0），B（0，1），有一组抛物线Ln，它们的顶点Cn（Xn，Yn）在直线AB上，并且经过点（Xn+1，0），当n=1，2，3，4，5…时，Xn=2，3，5，8，13…，根据上述规律，写出抛物线L1的表达式为
     
    ，抛物线L6的顶点坐标为
     
    ，抛物线L6与x轴的交点坐标为
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    问题背景：
    （1）如图（1），AD是△ABC的中线，将△ABD绕点D逆时针旋转得到△EFD．已知△ABC的面积为6，依题意填空：①∠ADC+∠EDF的度数为
     
    ；②△EFD的面积为
     
    ；
    探究发现：
    （2）如图（2），在△ABC和△BDE中，∠ABC+∠DBE=180°，且BA=BD，BC=BE．设△ABC的面积为S1，△BDE的面积为S2，求证：S1=S2；
    迁移运用：
    （3）如图（3），以Rt△ABC（∠ACB=90°）的三边为边长分别向外作正方形ABDE、BCGF、ACHM，连接DF、EM、GH．已知AB=5，BC=3，求六边形DEMHGF的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知点A（4，3）和点B是坐标平面内的两个点，且它们关于直线x=-3对称，则平面内点B的坐标为（　　）
    A、（0，-3）
    B、（4，-9）
    C、（4，0）
    D、（-10，3）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （1）如图①，在Rt△ABC中，若AB=AC，AD=AE，∠BAD=40°，则∠EDC=
     
    ．
    （2）如图②，∠ACB=90°，E、F为AB上的点，AE=AC，BC=BF，则∠ECF=
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

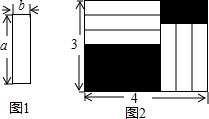    如图1是长为a，宽为b的小长方形卡片，把六张这样的小长方形卡片不重叠地放在一个底面为长方形（长为4，宽为3）的盒子底部（如图2），盒子底部未被卡片覆盖的部分用阴影表示，则图2中两块阴影部分的周长之和为（　　）
    A、8B、10C、12D、14

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    看图解答

    （1）通过观察比较左、右两图的阴影部分面积，可以得到乘法公式为
     
    ．
    （2）运用你所得到的公式，计算下题：
    ①10.3×9.7    
    ②（2m+n-p）（2m-n+p）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    小红爸爸上星期五买进某公司股票1000股，每股27元，下表为本周内每日该股票的涨跌情况．（单位：元）
    （1）通过上表你认为星期三收盘时，每股是多少？
    （2）本周内每股最高是多少？最低是多少元？
    （3）已知小红爸爸买进股票时付了1.5‰的手续费，卖出时还需付1.5‰的手续费和1‰的交易税，如果小红爸爸在星期五收盘时将全部股票卖出，请你对他的收益情况进行简单的评价？
    星期一二三四五
    每股涨跌+4+4.5-1-2.5-6

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如果3x=4y，那么x：y=
     
    ．

    查看答案和解析>>

    同步练习册答案