
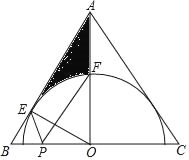
【题目】如图,在△ABC中,AB=AC,AO⊥BC于点O,OE⊥AB于点E,以点O为圆心,OE为半径作半圆,交AO于点F.
(1)求证:AC是⊙O的切线;
(2)若点F是OA的中点,OE=3,求图中阴影部分的面积;
(3)在(2)的条件下,点P是BC边上的动点,当PE+PF取最小值时,直接写出BP的长.
【答案】(1)详见解析;(2)![]() ;(3)当PE+PF取最小值时,BP的长为
;(3)当PE+PF取最小值时,BP的长为![]() .
.
【解析】
(1)作OH⊥AC于H,如图,利用等腰三角形的性质得AO平分∠BAC,再根据角平分线性质得OH=OE,然后根据切线的判定定理得到结论;
(2)先确定∠OAE=30°,∠AOE=60°,再计算出AE=3![]() ,然后根据扇形面积公式,利用图中阴影部分的面积=S△AOE-S扇形EOF进行计算;
,然后根据扇形面积公式,利用图中阴影部分的面积=S△AOE-S扇形EOF进行计算;
(3)作F点关于BC的对称点F′,连接EF′交BC于P,如图,利用两点之间线段最短得到此时EP+FP最小,通过证明∠F′=∠EAF′得到PE+PF最小值为3![]() ,然后计算出OP和OB得到此时PB的长.
,然后计算出OP和OB得到此时PB的长.
(1)证明:作OH⊥AC于H,如图,

∵AB=AC,AO⊥BC于点O,
∴AO平分∠BAC,
∵OE⊥AB,OH⊥AC,
∴OH=OE,
∴AC是⊙O的切线;
(2)∵点F是AO的中点,
∴AO=2OF=6,
而OE=3,
∴∠OAE=30°,∠AOE=60°,
∴AE=![]() OE=3
OE=3![]() ,
,
∴图中阴影部分的面积=S△AOE﹣S扇形EOF=![]() ×3×3
×3×3![]() ﹣
﹣![]() ;
;
(3)作F点关于BC的对称点F′,连接EF′交BC于P,如图,
∵PF=PF′,
∴PE+PF=PE+PF′=EF′,此时EP+FP最小,
∵OF′=OF=OE,
∴∠F′=∠OEF′,
而∠AOE=∠F′+∠OEF′=60°,
∴∠F′=30°,
∴∠F′=∠EAF′,
∴EF′=EA=3![]() ,
,
即PE+PF最小值为3![]() ,
,
在Rt△OPF′中,OP=![]() OF′=
OF′=![]() ,
,
在Rt△ABO中,OB=![]() OA=
OA=![]() ×6=2
×6=2![]() ,
,
∴BP=2![]() ﹣
﹣![]() =
=![]() ,
,
即当PE+PF取最小值时,BP的长为![]() .
.


科目:初中数学 来源: 题型:
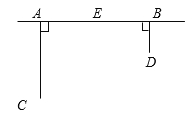
【题目】为丰富少年儿童的业余文化生活,某社区要在如图所示的AB所在的直线上建一图书阅览室,该社区有两所学校,所在的位置分别在点C和点D处。CA⊥AB于A,DB⊥AB于B,已知AB=25km,CA=15km,DB=10km,试问:阅览室E建在距A点多远时,才能使它到C、D两所学校的距离相等?
查看答案和解析>>
科目:初中数学 来源: 题型:
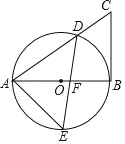
【题目】如图,AB是⊙O的直径,弦DE交AB于点F,⊙O的切线BC与AD的延长线交于点C,连接AE.
(1)试判断∠AED与∠C的数量关系,并说明理由;
(2)若AD=3,∠C=60°,点E是半圆AB的中点,则线段AE的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学校的社会实践活动中,一批学生协助搬运初一、二两个年级的图书,初一年级需要搬运的图书数量是初二年级需要搬运的图书数量的两倍.上午全部学生在初一年级搬运,下午一半的学生仍然留在初一年级(上下午的搬运时间相等)搬运,到放学时刚好把初一年级的图书搬运完.下午另一半的学生去初二年级搬运图书,到放学时还剩下一小部分未搬运,最后由三个学生再用一整天的时间刚好搬运完.如果这批学生每人每天搬运的效率是相同的,则这批学生共有人数为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
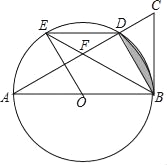
【题目】如图,以△ABC的边AB为直径画⊙O,交AC于点D,半径OE∥BD,连接BE,DE,BD,设BE交AC于点F,若∠DEB=∠DBC.
(1)求证:BC是⊙O的切线;
(2)若BF=BC=2,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读探索:“任意给定一个矩形A,是否存在另一个矩形B,它的周长和面积分别是已知矩形周长和面积的一半?”(完成下列空格)
(1)当已知矩形A的边长分别为6和1时,小亮同学是这样研究的:
设所求矩形的两边分别是x和y,由题意得方程组: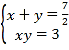 ,消去y化简得:2x2﹣7x+6=0,
,消去y化简得:2x2﹣7x+6=0,
∵△=49﹣48>0,
∴x1=_____,x2=_______,
∴满足要求的矩形B存在.
(2)如果已知矩形A的边长分别为2和1,请你仿照小亮的方法研究是否存在满足要求的矩形B.
(3)如果矩形A的边长为m和n,请你研究满足什么条件时,矩形B存在?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小聪和小明沿同一条路同时从学校出发到某超市购物,学校与超市的路程是4千米.小聪骑自行车,小明步行,当小聪从原路回到学校时,小明刚好到达超市.图中折线O﹣A﹣B﹣C和线段OD分别表示两人离学校的路程s(千米)与所经过的时间t(分钟)之间的函数关系,请根据图象回答下列问题:
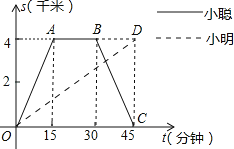
(1)小聪在超市购物的时间为 分钟,小聪返回学校的速度为 千米/分钟;
(2)请你求出小明离开学校的路程s(千米)与所经过的时间t(分钟)之间的函数关系式;
(3)当小聪与小明迎面相遇时,他们离学校的路程是多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 、
、![]() 在函数
在函数![]() (
(![]() ,
,![]() 且
且![]() 是常数)的图像上,且点
是常数)的图像上,且点![]() 在点
在点![]() 的左侧过点
的左侧过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,过点
,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,
,![]() 与
与![]() 的交点为
的交点为![]() ,连结
,连结![]() 、
、![]() .若
.若![]() 和
和![]() 的面积分别为1和4,则
的面积分别为1和4,则![]() 的值为( )
的值为( )

A.4B.![]() C.
C.![]() D.6
D.6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com