
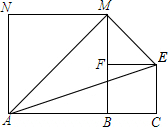 如图,线段AC=n+1(其中n为正整数),点B在线段AC上,在线段AC同侧作正方形ABMN及正方形BCEF,连接AM、ME、EA得到△AME.当AB=1时,△AME的面积记为S1;当AB=2时,△AME的面积记为S2;…;当AB=n时,△AME的面积记为Sn.则Sn=$\frac{1}{2}$n2.
如图,线段AC=n+1(其中n为正整数),点B在线段AC上,在线段AC同侧作正方形ABMN及正方形BCEF,连接AM、ME、EA得到△AME.当AB=1时,△AME的面积记为S1;当AB=2时,△AME的面积记为S2;…;当AB=n时,△AME的面积记为Sn.则Sn=$\frac{1}{2}$n2. 分析 将△AME的面积表示为长方形减去三个三角形的形式,根据题意,找出各边长度,根据长方形的面积,三角形的面积公式即可得出结论.
解答 解: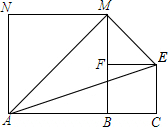 S△AME=AC•AN-$\frac{1}{2}$AN•MN-$\frac{1}{2}$AC•CE-$\frac{1}{2}$EF•MF.
S△AME=AC•AN-$\frac{1}{2}$AN•MN-$\frac{1}{2}$AC•CE-$\frac{1}{2}$EF•MF.
∵AB=n,BC=1,四边形ABMN及四边形BCEF均为正方形,
∴AN=MN=AB=n,EF=CE=BC=1,MF=BM-BF=n-1.
∴Sn=n(n+1)-$\frac{1}{2}$n•n-$\frac{1}{2}$(n+1)-$\frac{1}{2}$(n-1)=$\frac{1}{2}$n2.
故答案为:$\frac{1}{2}$n2
点评 本题考查了正方形的性质、长方形和三角形的面积公式,解题的关键是将△AME的面积表示为长方形减去三个三角形的形式.本题属于中档题,有点难度,由于△AMF不是特殊的三角形,故不能直角找出它的面积,需要利用分割长方形的方法才能得到结论.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
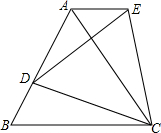 如图,△ABC是等边三角形,D是AB边上一点,以CD为边作等边△CDE,使点E、A在直线DC的同侧,连接AE,判断AE与BC的位置关系,并说明理由.
如图,△ABC是等边三角形,D是AB边上一点,以CD为边作等边△CDE,使点E、A在直线DC的同侧,连接AE,判断AE与BC的位置关系,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
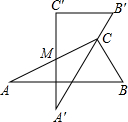 如图是两块完全一样的含30°角的直角三角板,将它们重叠在一起并绕其较长直角边的中点M转动,使上面一块三角板的斜边刚好过下面一块三角板的直角顶点C.已知AC=5,则这块直角三角板顶点A、A′之间的距离等于2.5.
如图是两块完全一样的含30°角的直角三角板,将它们重叠在一起并绕其较长直角边的中点M转动,使上面一块三角板的斜边刚好过下面一块三角板的直角顶点C.已知AC=5,则这块直角三角板顶点A、A′之间的距离等于2.5.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
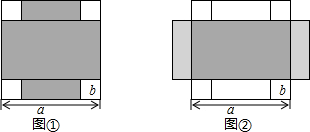
| A. | a2-4b2 | B. | (a+b)(a-b) | C. | (a+2b)(a-b) | D. | (a+b)(a-2b) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=(x-1)2+3 | B. | y=(x+1)2+3 | C. | y=(x+1)2-3 | D. | y=(x-1)2-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
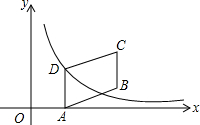 如图,四边形ABCD是平行四边形,点A(1,0)、B(3,1)、C(3,3),反比例函数y=$\frac{m}{x}$(x>0)的图象经过点D,则m=2.
如图,四边形ABCD是平行四边形,点A(1,0)、B(3,1)、C(3,3),反比例函数y=$\frac{m}{x}$(x>0)的图象经过点D,则m=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com