
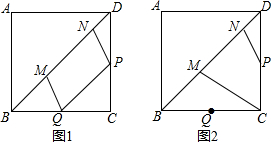
分析 (1)欲证明四边形MQPN是平行四边形,只要证明MN=PQ,MN∥PQ,根据三角形中位线定理即可解决.
(2)存在,如图作点Q关于BD的对称点H,连接CH与BD交于点M,此时CM+PN最小.可以证明CM+PN=CH,求出CH即可解决问题.
解答 (1)证明:∵四边形ABCD是正方形,AB=2,
∴∠C=90°,BC=CD=AB=2,
∴BD=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,
∵BQ=QC,DP=PC,
∴PQ∥BD,PQ=$\frac{1}{2}$BD=$\sqrt{2}$,
∵MN=$\sqrt{2}$,
∴PQ=MN,PQ∥MN,
∴四边形MQPN是平行四边形.
(2)存在,利用如下,
解:如图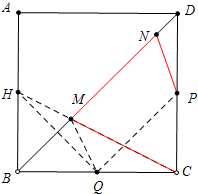 作点Q关于BD的对称点H,连接CH与BD交于点M,此时CM+PN最小.
作点Q关于BD的对称点H,连接CH与BD交于点M,此时CM+PN最小.
由(1)可知四边形MQPN是平行四边形,∴PN=MQ=HM,
∴PN+CM=NM+CM=CH,
根据两点之间线段最短可知PN+CM的最小值=CH,
在RT△BCH中,∵BH=BQ=1,BC=2,
∴HC=$\sqrt{B{H}^{2}+B{C}^{2}}$=$\sqrt{5}$.
∴PN+CM的最小值为$\sqrt{5}$.
点评 本题考查正方形的性质、平行四边形的判定和性质、轴对称等知识,学会利用对称解决最短问题,属于中考常考题型.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | (9m2+n2)(9n2+m2) | B. | (3m2+n2)(m+3n)(m-3n) | ||
| C. | (9m2+n)(3m-m)(3n-m) | D. | (3m+n)(3m-n)(3n+m)(3n-m) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
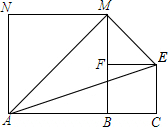 如图,线段AC=n+1(其中n为正整数),点B在线段AC上,在线段AC同侧作正方形ABMN及正方形BCEF,连接AM、ME、EA得到△AME.当AB=1时,△AME的面积记为S1;当AB=2时,△AME的面积记为S2;…;当AB=n时,△AME的面积记为Sn.则Sn=$\frac{1}{2}$n2.
如图,线段AC=n+1(其中n为正整数),点B在线段AC上,在线段AC同侧作正方形ABMN及正方形BCEF,连接AM、ME、EA得到△AME.当AB=1时,△AME的面积记为S1;当AB=2时,△AME的面积记为S2;…;当AB=n时,△AME的面积记为Sn.则Sn=$\frac{1}{2}$n2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com