
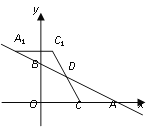
【题目】如图,一次函数y=-![]() x+m(m>0)的图像与x轴、y轴分别交于点A、B,点C在线段OA上,点C的横坐标为n,点D在线段AB上,且AD=2BD,将△ACD绕点D旋转180°后得到△A1C1D.
x+m(m>0)的图像与x轴、y轴分别交于点A、B,点C在线段OA上,点C的横坐标为n,点D在线段AB上,且AD=2BD,将△ACD绕点D旋转180°后得到△A1C1D.
(1)若点C1恰好落在y轴上,试求![]() 的值;
的值;
(2)当n=4时,若△A1C1D被y轴分得两部分图形的面积比为3:5,求该一次函数的解析式.
【答案】(1) ![]() ;(2)
;(2) ![]() 或
或![]()
【解析】试题分析:(1)由题意,得B(0,m),A(2m,0).过点D作x轴的垂线,交x轴于点E,交直线A1C1于点F,易求![]() 的值;
的值;
(2)由(1)得,当m>3时,点C1在y轴右侧;当2<m<3时,点C1在y轴左侧.分类讨论即可得解.
试题解析:(1)由题意,得B(0,m),A(2m,0).
如图,
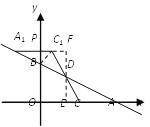
过点D作x轴的垂线,交x轴于点E,交直线A1C1于点F,
易知:DE=![]() m,D(
m,D(![]() m,
m, ![]() m) ,C1(
m) ,C1(![]() m-n,
m-n, ![]() m).
m).
∴![]() m-n=0,
m-n=0,
∴![]() =
=![]() ;
;
(2)由(1)得,当m>3时,点C1在y轴右侧;当2<m<3时,点C1在y轴左侧.
① 当m>3时,设A1C1与y轴交于点P,连接C1B,
由△A1C1D被y轴分得两部分图形的面积比为3:5,
∴S△BA1P:S△BC1P=3:1,
∴A1P:C1P=3,
∴![]() m=3(
m=3(![]() m-4),
m-4),
∴m=![]() .
.
∴y=-![]() x+
x+![]() .
.
② 当2<m<3时,同理可得:y=-![]() x+
x+![]() .
.
综上所述,y=-![]() x+
x+![]() 或y=-
或y=-![]() x+
x+![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,BD为□ABCD的对角线,按要求完成下列各题.

(1)用直尺和圆规作出对角线BD的垂直平分线交AD于点E,交BC于点F,垂足为O.(保留作图痕迹,不要求写作法)
(2)在(1)的基础上,连接BE和DF.求证:四边形BFDE是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,天平呈平衡状态,其中左侧秤盘中有一袋玻璃球,右侧秤盘中也有一袋玻璃球,还有2个各20克的砝码.现将左侧袋中一颗玻璃球移至右侧秤盘,并拿走右侧秤盘的1个砝码后,天平仍呈平衡状态,如图2,则被移动的玻璃球的质量为( )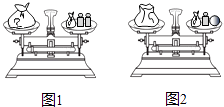
A.10克
B.15克
C.20克
D.25克
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式中,计算结果错误的是( )
A. (x+2)(x-3)=x2-x-6
B. (x-4)(x+4)=x2-16
C. (2x+3)(2x-6)=2x2-3x-18
D. (2x-1)(2x+2)=4x2+2x-2
查看答案和解析>>
科目:初中数学 来源: 题型:
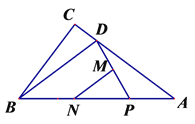
【题目】如图,在Rt△ABC中,∠C=90°AB=8cm,cos∠ABC=![]() ,点D在边AC上,且CD=
,点D在边AC上,且CD=![]() cm,动点P从点A开始沿边AB向点B以1cm/s的速度移动,当点P到达B点即停止运动.设运动时间为t(s).解答下列问题:
cm,动点P从点A开始沿边AB向点B以1cm/s的速度移动,当点P到达B点即停止运动.设运动时间为t(s).解答下列问题:
(1)M、N分别是DP、BP的中点,连接MN.
①分别求BC、MN的值;
②求在点P从点A匀速运动到点B的过程中线段MN所扫过区域的面积;
(2)在点P运动过程中,是否存在某一时刻t,使BD平分∠CDP?若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知ABCD,给出下列条件:①AC=BD;②∠BAD=90°;③AB=BC;④AC⊥BD,添加其中之一能使ABCD成为菱形的条件是( )
A. ①③ B. ②③ C. ③④ D. ①②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com