
【题目】(6分)株洲五桥主桥主孔为拱梁钢构组合体系(如图1),小明暑假旅游时,来到五桥观光,发现拱梁的路面部分有均匀排列着9根支柱,他回家上网查到了拱梁是抛物线,其跨度为20米,拱高(中柱)10米,于是他建立如图2的坐标系,发现可以将余下的8根支柱的高度都算出来了,请你求出中柱左边第二根支柱CD的高度.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
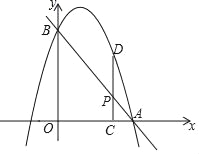
【题目】如图,已知直线y=﹣2x+4分别交x轴、y轴于点A、B,抛物线过A,B两点,点P是线段AB上一动点,过点P作PC⊥x轴于点C,交抛物线于点D.
(1)若抛物线的解析式为y=﹣2x2+2x+4,设其顶点为M,其对称轴交AB于点N.
①求点M、N的坐标;
②是否存在点P,使四边形MNPD为菱形?并说明理由;
(2)当点P的横坐标为1时,是否存在这样的抛物线,使得以B、P、D为顶点的三角形与△AOB相似?若存在,求出满足条件的抛物线的解析式;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某童装专卖店为了吸引顾客,在“六一”儿童节当天举办了甲、乙两种品牌童装有奖酬宾活动,凡购物满100元,均可得到一次摇奖的机会.已知在摇奖机内装有2个红球和2个白球,它们除颜色外其他都相同.摇奖者必须从摇奖机内一次连续摇出两个球,根据球的颜色决定送多少元的礼品券(如下表).
甲种品牌童装 | |||
球 | 两红 | 一红一白 | 两白 |
礼品券(元) | 15 | 30 | 15 |
乙种品牌童装 | |||
球 | 两红 | 一红一白 | 两白 |
礼品券(元) | 30 | 15 | 30 |
(1)请你用列表法或画树状图法求一次连续摇出一红一白两球的概率;
(2)如果一个顾客当天在本店购物满100元,请你帮助分析选择购买哪种品牌的童装对于顾客更合算,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,I是△ABC的内心,∠BAC的平分线与△ABC的外接圆相交于点D,交BC于点E.
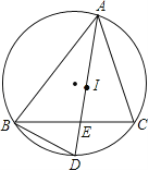
(1)求证:BD=ID;
(2)求证:ID2=DEDA.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:
X | ﹣1 | 0 | 1 | 3 |
y | ﹣1 | 3 | 5 | 3 |
下列结论:
⑴ac<0;
⑵当x>1时,y的值随x值的增大而减小.
⑶3是方程ax2+(b﹣1)x+c=0的一个根;
⑷当﹣1<x<3时,ax2+(b﹣1)x+c>0.
其中正确的个数为()
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象经过点(x1,0)、(2,0),且﹣2<x1<﹣1,与y轴正半轴的交点在(0,2)的下方,则下列结论:
①abc<0;②b2>4ac;③2a+b+1<0;④2a+c>0.
则其中正确结论的序号是
A. ①② B. ②③ C. ①②④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
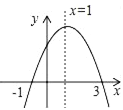
【题目】如图为二次函数y=ax2+bx+c的图象,给出下列说法:
①ab>0;
②方程ax2+bx+c=0的根为x1=﹣1,x2=3;
③a+b+c>0;
④当x>1时,随x值的增大而增大.
其中正确的说法有______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,CD是边AB上的高线,且有2CD=3AB=6,CE=EF=DF,则下列判断中不正确的是( )

A. ∠AFB=90 B. BE=![]() C. △EFB∽△BFC D. ∠ACB+∠AEB=45°
C. △EFB∽△BFC D. ∠ACB+∠AEB=45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC,且∠DCE=∠B.那么下列各判断中,错误的是( )

A. △ADE∽△ABC B. △ADE∽△ACD
C. △DEC∽△CDB D. △ADE∽△DCB
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com