练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    3．如图，CA⊥AB，CA=AB，DA=AE，BD=CE，求证：DA⊥EA．

    分析 根据全等三角形的判定和性质即可得到结论．

    解答 证明：在△ACE与△ABD中，$\left\{\begin{array}{l}{AC=AB}\\{AE=AD}\\{CE=BD}\end{array}\right.$，
    ∴△ACE≌△ABD，
    ∴∠EAC=∠DAB，
    ∴∠DAE=∠BAC，
    ∵CA⊥AB，
    ∴∠BAC=90°，
    ∴∠DAE=90°，
    ∴DA⊥EA．

    点评 此题考查全等三角形的判定和性质，熟练掌握全等三角形的判定和性质是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    13．已知2x6y2和-3x3my2是同类项，则m的值是（　　）
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．解方程：$\frac{2}{x-1}$-$\frac{1}{4-x}$=0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．如图，AB是⊙O的直径，弦CD⊥AB于点E．，AM是△ACD的外角∠DAF的平分线．
    （1）求证：.4M是⊙O的切线；
    （2）若∠D=60°，AD=2，射线CO与AM交于N点，请写出求ON长的思路．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．如图，在菱形ABCD中，E为AD边的中点，BE与对角线AC交于点F，过点F作FG⊥AB，垂足为点G．
    （1）求证：FC=2AF；
    （2）若∠1=∠2，CD=2$\sqrt{3}$，求FG的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．已知$\frac{x}{y+z}$=$\frac{y}{z+x}$=$\frac{z}{x+y}$，求分式$\frac{x+y+z}{x}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    15．某校为了了解七年级学生的体能情况，随机抽查了其中的30名学生，测试了1分钟仰卧起坐的次数，并绘制了图中所示的频数分布直方图，请根据图示计算，仰卧起坐次数在15-20（不含20）次的频数是3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

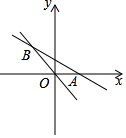    12．如图，已知直线y1=-$\frac{1}{2}$x+1与x轴交于点A，与直线y2=-$\frac{3}{2}$x交于点B．
    （1）求点A、B的坐标；
    （2）求△AOB的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．青少年“心理健康“问题越来越引起社会的关注，某中学为了了解学校600名学生的心理健康状况，举行了一次“心理健康“知识测试．并随机抽取了部分学生的成绩（得分取正整数，满分为100分）作为样本，绘制了下面未完成的频数分布表和频数分布直方图（如图）．请回答下列问题：
    分组频数频率
    50.5～60.540.08
    60.5～70.5140.28
    70.5～80.5160.32
    80.5～90.560.12
    90.5～100.5100.20
    合计501.00
    （1）填写频数分布表中的空格，并补全频数分布直方图；
    （2）若成绩在70分以上（不含70分）为心理健康状况良好．若心理健康状况良好的人数占总人数的70%以上，就表示该校学生的心理健康状况正常，否则就需要加强心理辅导．请根据上述数据分析该校学生是否需要加强心理辅导，并说明理由．

    查看答案和解析>>

    同步练习册答案