

���� ��1���ӳ�AE��BD��F�����ݡ�ACE�ա�DCB�����ɵó�AE=DB����CAE=��CDB�������õ���DFE=90�㣬��AE��DB��
��2�����ݡ�ACD�͡�BCE�ǵ���ֱ�������Σ��ж���ACE�ա�DCB ��SAS�������ɵõ�AE=BD����EAC=��BDC�����ӳ�AE��BD�ڵ�F�������������ڽǺͶ������ó���DFA=90�㣬���ɵõ�AE��BD��
��3������C��CF��CG����CF=CG������HF��EF���ж���BCG�ա�ECF��SAS�������ɵó�BG=EF����CBG=��CEF=45�㣬���ж���GCH�ա�FCH��SAS�������ɵõ�GH=FH����Rt��HEF�У����ݹ��ɶ����ó�EF2+HE2=FH2�������õ�BG2+HE2=GH2��
��� 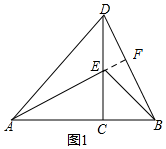 �⣺��1����ͼ1���ӳ�AE��BD��F��
�⣺��1����ͼ1���ӳ�AE��BD��F��
���ݵ���ֱ��������ACD�͵���ֱ��������BCE��
�ɵ�AC=DC����ACE=��DCB��EC=BC��
�á�ACE�ա�DCB��
��AE=DB����CAE=��CDB��
�֡ߡ�ACE=90�㣬��AEC=��DEF��
���DFE=90�㣬
��AF��DB����AE��DB��
���߶�AE ��BD��������ϵ��AE=BD��λ�ù�ϵ�� AE��BD��
�ʴ�Ϊ��AE=BD��AE��BD��
��2������AE=BD��AE��BD��Ȼ������
֤�����ߡ�ACD�͡�BCE�ǵ���ֱ�������Σ���ACD=��BCE=90��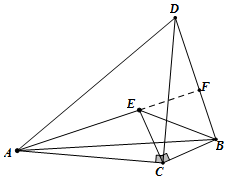 ��
��
��AC=CD��CE=CB��
�֡ߡ�ACE+��ECD=90�㣬��BCD+��ECD=90�㣬
���ACE=��BCD��
�ڡ�ACE�͡�DCB �У�
$\left\{\begin{array}{l}{AC=CD}\\{��ACE=��BCD}\\{CE=CB}\end{array}\right.$��
���ACE�ա�DCB ��SAS����
��AE=BD����EAC=��BDC��
��ͼ2���ӳ�AE��BD�ڵ�F��
�ߡ�ACD=90�㣬
���DAC+��ADC=90�㣬
�֡ߡ�ADF+��DAF+��DFA=180�㣬
���ADC+��BDC+��DAF+��DFA=180�㣬
���ADC+��EAC+��DAF+��DFA=180�㣬
���ADC+��DAC+��DFA=180�㣬
��90��+��DFA=180�㣬
���DFA=90�㣬
��AE��BD��
��3��BG��GH��HE��������ϵ�� BG2+HE2=GH2��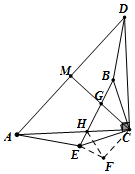
֤������ͼ3������C��CF��CG����CF=CG������HF��EF��
��CF��CG��CE��CB��
���BCG=��ECF��
�ڡ�BCG�͡�ECF�У�
$\left\{\begin{array}{l}{CF=CG}\\{��BCG=��ECF}\\{CE=CB}\end{array}\right.$��
���BCG�ա�ECF��SAS����
��BG=EF����CBG=��CEF=45�㣬
���HEF=��HEC+��CEF=90�㣬
�֡ߡ�ACE�ա�DCB��
���ACE=��DCB��
���FCH=��ACE+��ECF=��DCB+��BCG=45�㣬
���GCH=��FCH��
�ڡ�GCH�͡�FCH�У�
$\left\{\begin{array}{l}{CF=CG}\\{��GCH=��FCH}\\{CH=CH}\end{array}\right.$��
���GCH�ա�FCH��SAS����
��GH=FH��
����Rt��HEF��EF2+HE2=FH2��
��BG2+HE2=GH2��
���� ���������������ۺ��⣬��Ҫ�����˵���ֱ�������ε����ʣ�ȫ�������ε��ж��������Լ����ɶ������ۺ�Ӧ�ã��������Ĺؼ����������߹���ֱ���������Լ�ȫ�������Σ������������ڽǺ͵���180���Լ�ȫ�������εĶ�Ӧ����Ƚ����Ƶ���


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� |  | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ȫ֤������
��ȫ֤�������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com