
分析 首先把括号内的式子通分相加,把除法转化为乘法,计算乘法即可化简,然后把x2-2x-3=0化成x2-2x=3的形式,代入求值即可.
解答 解:原式=$[{\frac{1}{x+2}+\frac{2}{{({x+2})({x-2})}}}]÷\frac{x^2}{x+2}$
=$[{\frac{x-2}{{({x+2})({x-2})}}+\frac{2}{{({x+2})({x-2})}}}]÷\frac{x^2}{x+2}$
=$[{\frac{x-2+2}{{({x+2})({x-2})}}}]÷\frac{x^2}{x+2}$
=$\frac{x}{{({x+2})({x-2})}}÷\frac{x^2}{x+2}$
=$\frac{x}{{({x+2})({x-2})}}•\frac{x+2}{x^2}$
=$\frac{1}{{x({x-2})}}$.
∵x2-2x-3=0
∴x2-2x=3,
∴原式=$\frac{1}{3}$.
点评 本题考查了分式的化简求值,正确对所求的分式进行通分、约分,正确进行化简是关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
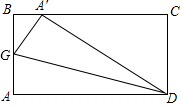 如图,ABCD是一张长方形纸片,且AD=2AB,沿过点D的折痕将A角翻折,使得点A落在BC上(如图中的点A′),折痕交AB于点G,则∠ADG=15度.
如图,ABCD是一张长方形纸片,且AD=2AB,沿过点D的折痕将A角翻折,使得点A落在BC上(如图中的点A′),折痕交AB于点G,则∠ADG=15度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com