
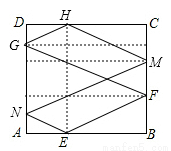
如图,正方形ABCD的边长为3,点E,F分别在边AB,BC上,AE=BF=1,小球P从点E出发沿直线向点F运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角.当小球P第一次碰到BC边时,小球P所经过的路程为 ;当小球P第一次碰到AD边时,小球P所经过的路程为 ;当小球P第n(n为正整数)次碰到点F时,小球P所经过的路程为 .

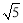 ,
,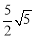 ,
,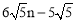 .
.
【解析】
试题分析:根据已知中的点E,F的位置,可知入射角的正切值为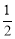 ,第一次碰撞点为F,在反射的过程中,根据入射角等于反射角及平行关系的三角形的相似可得第二次碰撞点为G,在DA上,且DG=
,第一次碰撞点为F,在反射的过程中,根据入射角等于反射角及平行关系的三角形的相似可得第二次碰撞点为G,在DA上,且DG=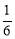 DA=
DA=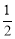 ,第三次碰撞点为H,在DC上,且DH=
,第三次碰撞点为H,在DC上,且DH= DC=1,第四次碰撞点为M,在CB上,且CM=
DC=1,第四次碰撞点为M,在CB上,且CM= BC=1,第五次碰撞点为N,在DA上,且AN=
BC=1,第五次碰撞点为N,在DA上,且AN=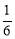 AD=
AD=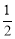 ,第六次回到E点,AE=
,第六次回到E点,AE= AB=1.
AB=1.
由勾股定理可以得出EF=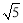 ,FG=
,FG=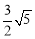 ,GH=
,GH=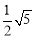 ,HM=
,HM=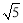 ,MN=
,MN=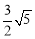 ,NE=
,NE=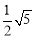 ,
,
∴当小球P第一次碰到AD边时,小球P所经过的路程为: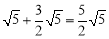 .
.
∴当小球P第2次碰到点F时,小球P所经过的路程为: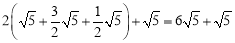 ;
;
当小球P第3次碰到点F时,小球P所经过的路程为: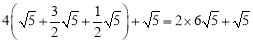 ;
;
当小球P第4次碰到点F时,小球P所经过的路程为: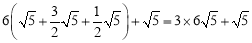 ;
;
……
当小球P第n(n为正整数)次碰到点F时,小球P所经过的路程为: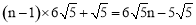 .
.
考点:1.探索规律题(图形的变化类――循环问题);2.跨学科问题3.正方形的性质;4.轴对称的性质;5.相似三角形的判定和性质;6.勾股定理.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源:2013-2014学年四川省眉山市华兴联谊学校九年级下学期期中考试数学试卷(解析版) 题型:选择题
下列运算,正确的是( )
A、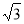 +
+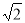 =
=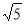 B、
B、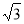 ×
×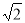 =
=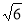
C、(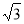 -1)2=3-1 D、
-1)2=3-1 D、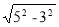 =5-3
=5-3
查看答案和解析>>
科目:初中数学 来源:2013-2014学年吉林省长春市朝阳区中考一模数学试卷(解析版) 题型:解答题
在一个不透明的盒子中放有三张卡片,分别标记为A、B、C,每张卡片除了标记不同外,其余均相同.某同学第一次从盒子中随机抽取一张卡片,卡片放回,第二次又随机抽取一张卡片.请用画树状图(或列表)的方法,求两次抽取的都是A的概率.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市顺义区中考二模数学试卷(解析版) 题型:解答题
在△ABC中, AB=AC ,∠A=300,将线段 BC 绕点 B 逆时针旋转 600得到线段 BD ,再将线段BD平移到EF,使点E在AB上,点F在AC上.
(1)如图 1,直接写出∠ABD和∠CFE的度数;
(2)在图1中证明:AE =CF;
(3)如图2,连接 CE ,判断△CEF的形状并加以证明.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市顺义区中考二模数学试卷(解析版) 题型:解答题
如图,在平面直角坐标系xOy中,一次函数 的图象与x轴交于点A,与y轴交于点B,已知
的图象与x轴交于点A,与y轴交于点B,已知 ,
, ,点C(-2,m)在直线AB上,反比例函数
,点C(-2,m)在直线AB上,反比例函数 的图象经过点C.
的图象经过点C.
(1)求一次函数及反比例函数的解析式;
(2)结合图象直接写出:当 时,不等式
时,不等式 的解集.
的解集.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市顺义区中考二模数学试卷(解析版) 题型:选择题
陈老师打算购买气球装扮学校“六一”儿童节活动会场,气球的种类有笑脸和爱心两种,两种气球的价格不同,但同一种气球的价格相同.由于会场布置需要,购买时以一束(4个气球)为单位,已知第一、二束气球的价格如图所示,则第三束气球的价格(单位:元)为( )

A.19 B.18 C.16 D.15
查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市顺义区中考一模数学试卷(解析版) 题型:解答题
设p,q都是实数,且 .我们规定:满足不等式
.我们规定:满足不等式 的实数x的所有取值的全体叫做闭区间,表示为
的实数x的所有取值的全体叫做闭区间,表示为 .对于一个函数,如果它的自变量x与函数值y满足:当
.对于一个函数,如果它的自变量x与函数值y满足:当 时,有
时,有 ,我们就称此函数是闭区间
,我们就称此函数是闭区间 上的“闭函数”.
上的“闭函数”.
(1)反比例函数 是闭区间
是闭区间 上的“闭函数”吗?请判断并说明理由;
上的“闭函数”吗?请判断并说明理由;
(2)若一次函数 是闭区间
是闭区间 上的“闭函数”,求此函数的解析式;
上的“闭函数”,求此函数的解析式;
(3)若实数c,d满足 ,且
,且 ,当二次函数
,当二次函数 是闭区间
是闭区间 上的“闭函数”时,求c,d的值.
上的“闭函数”时,求c,d的值.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市顺义区中考一模数学试卷(解析版) 题型:选择题
如图,点C为⊙O的直径AB上一动点,AB=2,过点C作DE⊥AB交⊙O于点D、E,连结AD,AE. 当点C在AB上运动时,设AC的长为x,△ADE的面积为y,下列图象中,能表示y与x的函数关系的图象大致是( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(黑龙江绥化卷)数学(解析版) 题型:解答题
如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠1=∠BCD.
(1)求证:CB//PD;
(2)若BC=3,sin∠BPD= ,求⊙O的直径.
,求⊙O的直径.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com