
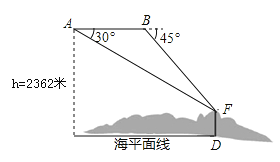
【题目】国家海洋局将中国钓鱼岛最高峰命名为“高华峰”,并对钓鱼岛进行常态化立体巡航.如图,在一次巡航过程中,巡航飞机飞行高度为2362米,在点A测得高华峰顶F点的俯角为30°,保持方向不变前进1464米到达B点后测得F点俯角为45°,请据此计算钓鱼岛的最高海拔高度多少米.(结果保留整数,参考数![]() =1.732,
=1.732,![]() =1.414)
=1.414)
科目:初中数学 来源: 题型:
【题目】我校计划在暑假期间对总面积为5400![]() 的塑胶操场进行改造,安排甲、乙两个工程队完成.已知甲队每天能完成改造的面积是乙队每天能完成改造的面积的2倍,并且在独立完成面积为1200
的塑胶操场进行改造,安排甲、乙两个工程队完成.已知甲队每天能完成改造的面积是乙队每天能完成改造的面积的2倍,并且在独立完成面积为1200![]() 区域的改造时,甲队比乙队少用10天.
区域的改造时,甲队比乙队少用10天.
(1)求甲、乙两工程队每天能完成操场改造的面积分别是多少![]() ?
?
(2)为方便管理,学校每天只允许一个工程队施工,若学校每天需付给甲队的施工费用为0.8万元,乙队为0.35万元,要使这次的改造在暑假50天期间完工,怎样安排才能使费用最省?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是菱形,DF⊥AB于点F,BE⊥CD于点E.
(1)求证:AF=CE;
(2)若DE=2,BE=4,求sin∠DAF的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
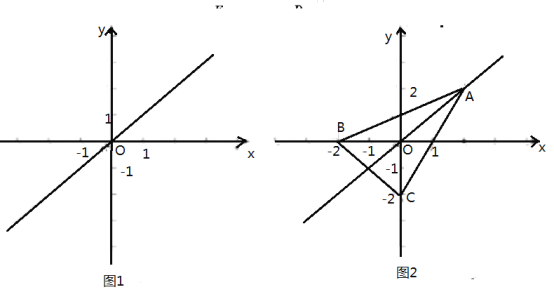
【题目】在平面直角坐标系![]() 中,对于点
中,对于点![]() 与图形
与图形![]() ,若点
,若点![]() 为图形
为图形![]() 上任意一点, 点
上任意一点, 点![]() 关于第一、三象限角平分线的对称点为
关于第一、三象限角平分线的对称点为![]() ,且线段
,且线段![]() 的中点为
的中点为![]() ,则称点
,则称点![]() 是图形
是图形![]() 关于点
关于点![]() 的“关联点”
的“关联点”
(1)如图1,若点![]() 是点
是点![]() 关于原点的关联点,则点
关于原点的关联点,则点![]() 的坐标为
的坐标为
(2)如图2,在![]() 中,
中,![]()
①将线段![]() 向右平移
向右平移![]() 个单位长度,若平移后的线段上存在两个
个单位长度,若平移后的线段上存在两个![]() 关于点
关于点![]() 的关联点,则
的关联点,则![]() 的取值范围是
的取值范围是
②已知点![]() 和点
和点![]() ,若线段
,若线段![]() 上存在
上存在![]() 关于点
关于点![]() 的关联点,求
的关联点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】双十一购物节即将到来,某商场设计了两种的促销方案,并有以下两种销售量预期.预期一:第1步,销售量扩大为原来的a倍.第2步,再扩大为第1步销售量的b倍.预期二:第1步,销售量扩大为原来的![]() 倍;第2步,再扩大为第1步销售量的
倍;第2步,再扩大为第1步销售量的![]() 倍;其中a,b为不相等的正数,请问两种预期中,哪种销售量更多?试说明理由.
倍;其中a,b为不相等的正数,请问两种预期中,哪种销售量更多?试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是48°. 若坡角∠FAE=30°,求大树的高度. (结果保留整数,参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11,![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
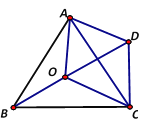
【题目】如图,点O是等边三角形ABC内一点,∠AOB=110°,∠BOC=β.将△BOC绕点C按顺时针方向旋转60°得到△ADC,连接OD.
(1)求证:△COD是等边三角形;
(2)当β=150°时,试判断△AOD的形状,并说明理由;
(3)探究:当β为多少度时,△AOD是以OD为底边的等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,它与x轴的两个交点分别为(-1,0),(3,0).对于下列命题:①b-2a=0;②abc<0;③4a-2b+c<0.其中正确的有( )
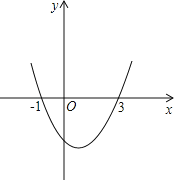
A. 3个 B. 2个 C. 1个 D. 0个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CN是等边△![]() 的外角
的外角![]() 内部的一条射线,点A关于CN的对称点为D,连接AD,BD,CD,其中AD,BD分别交射线CN于点E,P.
内部的一条射线,点A关于CN的对称点为D,连接AD,BD,CD,其中AD,BD分别交射线CN于点E,P.
(1)依题意补全图形;
(2)若![]() ,求
,求![]() 的大小(用含
的大小(用含![]() 的式子表示);
的式子表示);
(3)用等式表示线段![]() ,
, ![]() 与
与![]() 之间的数量关系,并证明.
之间的数量关系,并证明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com