
【题目】在平面直角坐标系![]() 中,对于点
中,对于点![]() 与图形
与图形![]() ,若点
,若点![]() 为图形
为图形![]() 上任意一点, 点
上任意一点, 点![]() 关于第一、三象限角平分线的对称点为
关于第一、三象限角平分线的对称点为![]() ,且线段
,且线段![]() 的中点为
的中点为![]() ,则称点
,则称点![]() 是图形
是图形![]() 关于点
关于点![]() 的“关联点”
的“关联点”
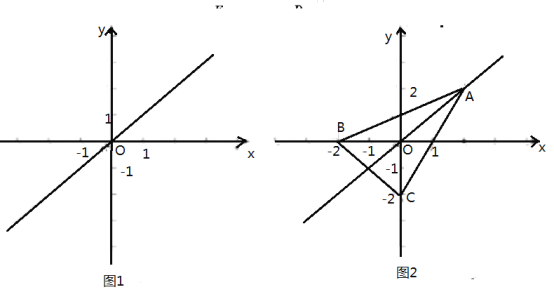
(1)如图1,若点![]() 是点
是点![]() 关于原点的关联点,则点
关于原点的关联点,则点![]() 的坐标为
的坐标为
(2)如图2,在![]() 中,
中,![]()
①将线段![]() 向右平移
向右平移![]() 个单位长度,若平移后的线段上存在两个
个单位长度,若平移后的线段上存在两个![]() 关于点
关于点![]() 的关联点,则
的关联点,则![]() 的取值范围是
的取值范围是
②已知点![]() 和点
和点![]() ,若线段
,若线段![]() 上存在
上存在![]() 关于点
关于点![]() 的关联点,求
的关联点,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②
;②![]() 或
或![]() .
.
【解析】
(1)设点P坐标为(a,b),根据“关联点”的定义、中点的坐标公式和关于第一、三象限角平分线对称的两点的坐标规律即可;
(2)①先求出原AC与x轴的交点,然后根据△ABC是轴对称图形,且对称轴为第一、三象限角平分线和“关联点”的定义可得:“关联点”定义中的![]() 为OA关于(2,0)的对称线段
为OA关于(2,0)的对称线段![]() 与△ABC边的交点,平移线段
与△ABC边的交点,平移线段![]() 可发现:当
可发现:当![]() 在C的左侧,
在C的左侧,![]() 过点(1,0)或(1,0)的右侧时符合题意,再列出不等式即可;
过点(1,0)或(1,0)的右侧时符合题意,再列出不等式即可;
②由S、T的坐标可知,线段ST是x轴的一部分,线段ST关于点N的对称线段![]() 也是x轴的一部分,从而判断出定义中
也是x轴的一部分,从而判断出定义中![]() 是△ABC边与x轴的交点,由图可知:点
是△ABC边与x轴的交点,由图可知:点![]() 只有(-2,0)与(1,0)两种可能,再根据线段
只有(-2,0)与(1,0)两种可能,再根据线段![]() 需要过点(-2,0)或(1,0)分类讨论并列出不等式即可.
需要过点(-2,0)或(1,0)分类讨论并列出不等式即可.
解:(1)设点P坐标为(a,b)
∵点![]() 关于第一、三象限角平分线的对称点为
关于第一、三象限角平分线的对称点为![]() ,
,
∴![]() ,
,
∵点![]() 是点
是点![]() 关于原点的关联点,
关于原点的关联点,
∴![]() 的中点为原点,
的中点为原点,
∴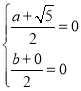 ,解得
,解得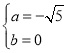
∴点P坐标为:![]()
故答案为:![]()
(2)①设原AC的解析式为y=kx+b,
将![]() 代入得:
代入得:
![]() ,解得:
,解得:![]()
∴原直线AC的解析式为:y=2x-2,
当y=0时,解得:x=1,
∴原AC与x轴的交点为(1,0)
△ABC是轴对称图形,且对称轴为第一、三象限角平分线和“关联点”的定义可得:定义中的Q在△ABC边上,
∴![]() 也在△ABC的边上,
也在△ABC的边上,
∵将线段AO向右平移d(d>0)个单位长度,若平移后的线段上存在两个△ABC关于点(2,0)的关联点,
∴点![]() 和线段OA上的点必关于点(2,0)对称,此时O点坐标为(d,0),A点坐标为(2+d,2),
和线段OA上的点必关于点(2,0)对称,此时O点坐标为(d,0),A点坐标为(2+d,2),
故作出OA关于(2,0)的对称线段![]() ,其中
,其中![]() ,
,![]() ,
,![]() 也必在
也必在![]() 上,即点
上,即点![]() 为
为![]() 与△ABC边的交点,
与△ABC边的交点,
∵平移后的线段上存在两个![]() 关于点
关于点![]() 的关联点,
的关联点,
∴![]() 与△ABC边必须有两个交点才满足题意,
与△ABC边必须有两个交点才满足题意,
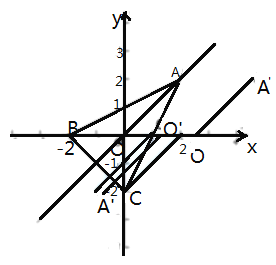
如图中蓝线所示,平移![]() 可发现,当
可发现,当![]() 与C重合时,与△ABC边有一个交点,继续向左平移即可有两个交点,当
与C重合时,与△ABC边有一个交点,继续向左平移即可有两个交点,当![]() 过点(1,0)也有两个交点,继续向左平移就只有一个交点,
过点(1,0)也有两个交点,继续向左平移就只有一个交点,
故当![]() 在C的左侧,
在C的左侧,![]() 过点(1,0)或(1,0)的右侧时符合题意,
过点(1,0)或(1,0)的右侧时符合题意,
![]() ,解得:
,解得:![]() .
.
故答案为:![]()
②∵点![]() 和点
和点![]()
∴线段ST是x轴的一部分
∴线段ST上存在△ABC关于点N(n,0)的关联点,
故S、T关于点N(n,0)的对称点![]() 坐标为(n-2,0),
坐标为(n-2,0),![]() 坐标为(n-4,0)定义中
坐标为(n-4,0)定义中![]() 在线段
在线段![]() 上,
上,
∴![]() 即为△ABC边与x轴的交点,
即为△ABC边与x轴的交点,
由图可知,点![]() 只有(-2,0)与(1,0)两种可能,
只有(-2,0)与(1,0)两种可能,
∴线段![]() 需要过点(-2,0)或(1,0),
需要过点(-2,0)或(1,0),
当线段![]() 需要过点(-2,0)时,
需要过点(-2,0)时,
![]() ,解得
,解得![]()
当线段![]() 需要过点(1,0)时,
需要过点(1,0)时,
![]() ,解得
,解得![]() ,
,
综上所述:![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于点P(a,b)和点Q(a,b′),给出如下定义:
若b′=![]() ,则称点Q为点P的限变点.例如:点(2,3)的限变点的坐标是(2,3),点(-2,5)的限变点的坐标是(-2,-5).
,则称点Q为点P的限变点.例如:点(2,3)的限变点的坐标是(2,3),点(-2,5)的限变点的坐标是(-2,-5).
(1)①点(![]() ,1)的限变点的坐标是 ;
,1)的限变点的坐标是 ;
②在点A(-2,-1),B(-1,2)中有一个点是函数y=![]() 图象上某一个点的限变点,这个点是 ;(填“A”或“B”)
图象上某一个点的限变点,这个点是 ;(填“A”或“B”)
(2)若点P在函数y=-x+3(-2≤x≤k,k>-2)的图象上,其限变点Q的纵坐标b′的取值范围是-5≤b′≤2,求k的取值范围 ;
(3)若点P在关于x的二次函数y=x2-2tx+t2+t的图象上,其限变点Q的纵坐标b′的取值范围是b′≥m或b′<n,其中m>n.令s=m-n,求s关于t的函数解析式及s的取值范围 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,E为BC上一点,连接AE,作EF⊥AE交AB于F.
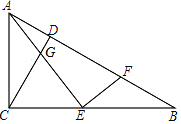
(1)求证:△AGC∽△EFB.
(2)除(1)中相似三角形,图中还有其它相似三角形吗?如果有,请把它们都写出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
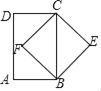
【题目】有一个边长为a的大正方形和四个边长为b的全等的小正方形(其中a>2b),按如图方式摆放,并顺次连接四个小正方形落入大正方形内部的顶点,得到四边形ABCD.
下面有四种说法:
①阴影部分周长为4a;
②阴影部分面积为(a+2b)(a-2b);
③四边形ABCD周长为8a-4b;
④四边形ABCD的面积为a24ab4b2.
所有合理说法的序号是____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,AD为中线,点P是AD上一点,点Q是AC上一点,且∠BPQ+∠BAQ=180°.
(1)若∠ABP=α,求∠PQC的度数(用含α的式子表示);
(2)求证:BP=PQ.

查看答案和解析>>
科目:初中数学 来源: 题型:
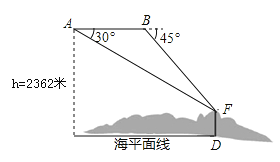
【题目】国家海洋局将中国钓鱼岛最高峰命名为“高华峰”,并对钓鱼岛进行常态化立体巡航.如图,在一次巡航过程中,巡航飞机飞行高度为2362米,在点A测得高华峰顶F点的俯角为30°,保持方向不变前进1464米到达B点后测得F点俯角为45°,请据此计算钓鱼岛的最高海拔高度多少米.(结果保留整数,参考数![]() =1.732,
=1.732,![]() =1.414)
=1.414)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论;
①b2-4ac<0②x<0时,y随x的增大而增大③a-b+c<0④abc>0⑤2a+b>0
其中,正确结论是______
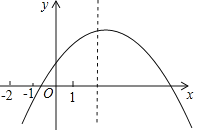
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD内有一点F,FB与FC分别平分∠ABC和∠BCD,点E为矩形ABCD外一点,连接BE,CE.现添加下列条件:①EB∥CF,CE∥BF;②BE=CE,BE=BF;③BE∥CF,CE⊥BE;④BE=CE,CE∥BF,其中能判定四边形BECF是正方形的共有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com