
【题目】有一个边长为a的大正方形和四个边长为b的全等的小正方形(其中a>2b),按如图方式摆放,并顺次连接四个小正方形落入大正方形内部的顶点,得到四边形ABCD.
下面有四种说法:
①阴影部分周长为4a;
②阴影部分面积为(a+2b)(a-2b);
③四边形ABCD周长为8a-4b;
④四边形ABCD的面积为a24ab4b2.
所有合理说法的序号是____.

【答案】①②④.
【解析】
①利用平移法即可发现阴影部分的周长=大正方形的周长,计算大正方形的周长即可;
②用大正方形的面积减去四个小正方形的面积即可;
③先证出四边形ABCD是正方形,然后计算出ABCD的边长,即可计算它的周长;
④根据③中的边长求面积即可.
解:①如下图所示:利用平移法可发现:阴影部分的周长=大正方形的周长=4a,
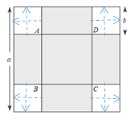
故①正确;
②阴影部分的面积=大正方形的面积-四个小正方形的面积= a2b2=(a+2b)(a-2b)
故②正确;
③由图可知:AB=a-2b,AD=a-2b,∠BAD=90°
∴四边形ABCD是正方形,
∴四边形ABCD的周长为:4(a-2b)=4a-8b
故③错误;
④正方形ABCD的面积为:(a-2b)2= a24ab4b2
故④正确.
故答案为:①②④.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为a,射线AM是∠A外角的平分线,点E在边AB上运动(不与点A、B重合),点F在射线AM上,且AF=√2BE,CF与AD相交于点G,连结EC、EF、EG.
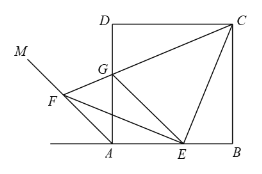
(1)求证:CE=EF;
(2)求△AEG的周长(用含a的代数式表示)
(3)试探索:点E在边AB上运动至什么位置时,△EAF的面积最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是菱形,DF⊥AB于点F,BE⊥CD于点E.
(1)求证:AF=CE;
(2)若DE=2,BE=4,求sin∠DAF的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,对于点
中,对于点![]() 与图形
与图形![]() ,若点
,若点![]() 为图形
为图形![]() 上任意一点, 点
上任意一点, 点![]() 关于第一、三象限角平分线的对称点为
关于第一、三象限角平分线的对称点为![]() ,且线段
,且线段![]() 的中点为
的中点为![]() ,则称点
,则称点![]() 是图形
是图形![]() 关于点
关于点![]() 的“关联点”
的“关联点”
(1)如图1,若点![]() 是点
是点![]() 关于原点的关联点,则点
关于原点的关联点,则点![]() 的坐标为
的坐标为
(2)如图2,在![]() 中,
中,![]()
①将线段![]() 向右平移
向右平移![]() 个单位长度,若平移后的线段上存在两个
个单位长度,若平移后的线段上存在两个![]() 关于点
关于点![]() 的关联点,则
的关联点,则![]() 的取值范围是
的取值范围是
②已知点![]() 和点
和点![]() ,若线段
,若线段![]() 上存在
上存在![]() 关于点
关于点![]() 的关联点,求
的关联点,求![]() 的取值范围.
的取值范围.
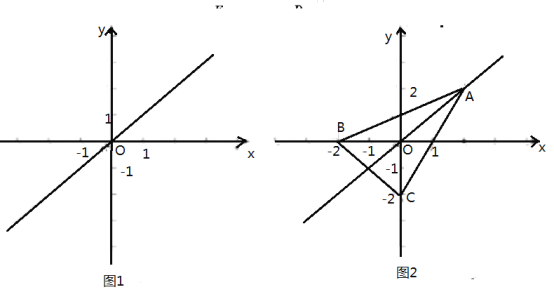
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】双十一购物节即将到来,某商场设计了两种的促销方案,并有以下两种销售量预期.预期一:第1步,销售量扩大为原来的a倍.第2步,再扩大为第1步销售量的b倍.预期二:第1步,销售量扩大为原来的![]() 倍;第2步,再扩大为第1步销售量的
倍;第2步,再扩大为第1步销售量的![]() 倍;其中a,b为不相等的正数,请问两种预期中,哪种销售量更多?试说明理由.
倍;其中a,b为不相等的正数,请问两种预期中,哪种销售量更多?试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是等边三角形ABC内一点,∠AOB=110°,∠BOC=β.将△BOC绕点C按顺时针方向旋转60°得到△ADC,连接OD.
(1)求证:△COD是等边三角形;
(2)当β=150°时,试判断△AOD的形状,并说明理由;
(3)探究:当β为多少度时,△AOD是以OD为底边的等腰三角形?
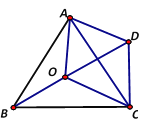
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,连结AC,过![]() 上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE.
上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE.
(1)求证:△ECF∽△GCE;
(2)求证:EG是⊙O的切线;
(3)延长AB交GE的延长线于点M,若tanG=![]() ,AH=
,AH=![]() ,求EM的值.
,求EM的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com