
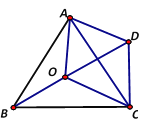
【题目】如图,点O是等边三角形ABC内一点,∠AOB=110°,∠BOC=β.将△BOC绕点C按顺时针方向旋转60°得到△ADC,连接OD.
(1)求证:△COD是等边三角形;
(2)当β=150°时,试判断△AOD的形状,并说明理由;
(3)探究:当β为多少度时,△AOD是以OD为底边的等腰三角形?
【答案】(1)证明见解析;(2)△AOD是直角三角形,理由见解析;(3)125°.
【解析】
(1)根据图形旋转的性质,得OC=DC,∠OCD=60°,进而即可得到结论;
(2)由等边三角形的性质得∠ODC=60°,结合∠ADC=∠BOC=β=150°,即可得到结论;
(3)由题意得∠AOD=β-60°,结合周角的定义,列出关于β的方程,即可求解.
(1)∵将△BOC绕点C按顺时针方向旋转60°得到△ADC,
∴ OC=DC,∠OCD=60°,
∴△COD是等边三角形;
(2)△AOD是直角三角形,理由如下:
∵△COD是等边三角形,
∴∠ODC=60°,
∵∠ADC=∠BOC=β=150°,
∴∠ADO=∠ADC-∠CDO=150°-60°=90°,
∴△AOD是直角三角形;
(3) ∵△AOD是以OD为底边的等腰三角形,
∴∠ADO=∠AOD=∠ADC-60°=β-60°,
∵110°+β+(60°+∠AOD)=360°,
∴110°+β+(60°+β-60°)=360°,
∴β=125°,
∴当β=125°时,△AOD是以OD为底边的等腰三角形.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:初中数学 来源: 题型:
【题目】“端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗.我市某食品厂为了解市民对去年销量较好的肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A、B、C、D表示)这四种不同口味粽子的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整).

请根据以上信息回答:
(1)本次参加抽样调查的居民有多少人?
(2)将两幅不完整的图补充完整;
(3)若居民区有8000人,请估计爱吃D粽的人数;
(4)若有外型完全相同的A、B、C、D粽各一个,煮熟后,小王吃了两个.用列表或画树状图的方法,求他第二个吃到的恰好是C粽的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个边长为a的大正方形和四个边长为b的全等的小正方形(其中a>2b),按如图方式摆放,并顺次连接四个小正方形落入大正方形内部的顶点,得到四边形ABCD.
下面有四种说法:
①阴影部分周长为4a;
②阴影部分面积为(a+2b)(a-2b);
③四边形ABCD周长为8a-4b;
④四边形ABCD的面积为a24ab4b2.
所有合理说法的序号是____.

查看答案和解析>>
科目:初中数学 来源: 题型:
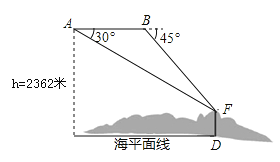
【题目】国家海洋局将中国钓鱼岛最高峰命名为“高华峰”,并对钓鱼岛进行常态化立体巡航.如图,在一次巡航过程中,巡航飞机飞行高度为2362米,在点A测得高华峰顶F点的俯角为30°,保持方向不变前进1464米到达B点后测得F点俯角为45°,请据此计算钓鱼岛的最高海拔高度多少米.(结果保留整数,参考数![]() =1.732,
=1.732,![]() =1.414)
=1.414)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中装有三个完全相同的小球,分别标有数字3、4、5.从袋子中随机取出一个小球,用小球上的数字作为十位的数字,然后放回;再取出一个小球,用小球上的数字作为个位上的数字,这样组成一个两位数,试问:按这种方法能组成哪些位数?十位上的数字与个位上的数字之和为9的两位数的概率是多少?用列表法或画树状图法加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论;
①b2-4ac<0②x<0时,y随x的增大而增大③a-b+c<0④abc>0⑤2a+b>0
其中,正确结论是______
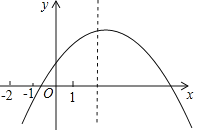
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在Rt△ABC中,∠C=90°,BD平分∠ABC,过D作DE⊥BD交AB于点E,经过B,D,E三点作⊙O.
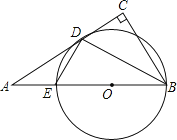
(1)求证:AC与⊙O相切于D点;
(2)若AD=15,AE=9,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则下列结论:①4ac﹣b2<0;②2a﹣b=0;③a+b+c<0;④点M(x1,y1)、N(x2,y2)在抛物线上,若x1<x2,则y1≤y2,其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
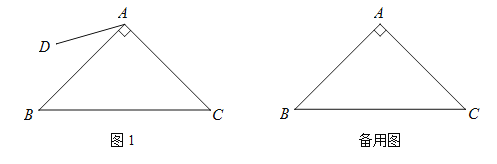
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=AC.在平面内任取一点D,连结AD(AD<AB),将线段AD绕点A逆时针旋转90°,得到线段AE,连结DE,CE,BD.
(1)请根据题意补全图1;
(2)猜测BD和CE的数量关系并证明;
(3)作射线BD,CE交于点P,把△ADE绕点A旋转,当∠EAC=90°,AB=2,AD=1时,补全图形,直接写出PB的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com