
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论;
①b2-4ac<0②x<0时,y随x的增大而增大③a-b+c<0④abc>0⑤2a+b>0
其中,正确结论是______
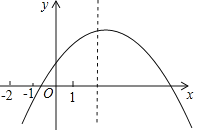
【答案】②③⑤
【解析】
利用抛物线与x轴有2个交点和判别式的意义对①进行判断;利用二次函数的性质对②进行判断;利用x=-1时,y<0可对③进行判断;由抛物线开口向下得到a<0,由抛物线的对称轴在y轴右侧得b>0,由抛物线与y轴的交点在x轴上方得c>0,则可对④进行判断;利用对称轴方程得到-![]() >1,则可对⑤进行判断.
>1,则可对⑤进行判断.
∵抛物线与x轴有2个交点,
∴△=b2-4ac>0,所以①错误;
∵x<0在对称轴的左侧,
∴y随x的增大而增大,所以②正确;
∵x=-1时,y<0,
∴a-b+c<0,所以③正确;
∵抛物线开口向下,
∴a<0,
∵抛物线的对称轴在y轴右侧,
∴a、b异号,即b>0,
∵抛物线与y轴的交点在x轴上方,
∴c>0,
∴abc<0,所以④错误;
∵-![]() >1,
>1,
而a<0,
∴b>-2a,即2a+b>0,所以⑤正确.
故答案为②③⑤.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】如图,等腰直角△ABC中,AC=BC,BE平分∠ABC,AD⊥BE的延长线于点D,若AD=2,则△ABE的面积为( ).
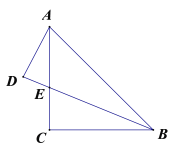
A.4B.6C.2![]() D.2
D.2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,对于点
中,对于点![]() 与图形
与图形![]() ,若点
,若点![]() 为图形
为图形![]() 上任意一点, 点
上任意一点, 点![]() 关于第一、三象限角平分线的对称点为
关于第一、三象限角平分线的对称点为![]() ,且线段
,且线段![]() 的中点为
的中点为![]() ,则称点
,则称点![]() 是图形
是图形![]() 关于点
关于点![]() 的“关联点”
的“关联点”
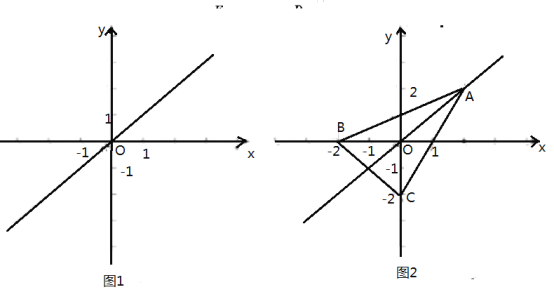
(1)如图1,若点![]() 是点
是点![]() 关于原点的关联点,则点
关于原点的关联点,则点![]() 的坐标为
的坐标为
(2)如图2,在![]() 中,
中,![]()
①将线段![]() 向右平移
向右平移![]() 个单位长度,若平移后的线段上存在两个
个单位长度,若平移后的线段上存在两个![]() 关于点
关于点![]() 的关联点,则
的关联点,则![]() 的取值范围是
的取值范围是
②已知点![]() 和点
和点![]() ,若线段
,若线段![]() 上存在
上存在![]() 关于点
关于点![]() 的关联点,求
的关联点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是48°. 若坡角∠FAE=30°,求大树的高度. (结果保留整数,参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11,![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是等边三角形ABC内一点,∠AOB=110°,∠BOC=β.将△BOC绕点C按顺时针方向旋转60°得到△ADC,连接OD.
(1)求证:△COD是等边三角形;
(2)当β=150°时,试判断△AOD的形状,并说明理由;
(3)探究:当β为多少度时,△AOD是以OD为底边的等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系上有点A(1,0),点A第一次跳动至点![]() ,第二次点
,第二次点![]() 跳动至点
跳动至点![]() 第三次点
第三次点![]() 跳动至点
跳动至点![]() ,第四次点
,第四次点![]() 跳动至点
跳动至点![]() ……,依此规律跳动下去,则点
……,依此规律跳动下去,则点![]() 与点
与点![]() 之间的距离是( )
之间的距离是( )

A. 2017B. 2018C. 2019D. 2020
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,它与x轴的两个交点分别为(-1,0),(3,0).对于下列命题:①b-2a=0;②abc<0;③4a-2b+c<0.其中正确的有( )
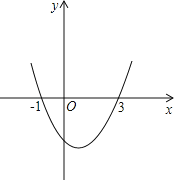
A. 3个 B. 2个 C. 1个 D. 0个
查看答案和解析>>
科目:初中数学 来源: 题型:
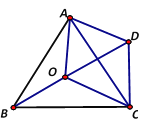
【题目】△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD为边在AD右侧作正方形ADEF,连接CF.
(1)观察猜想
如图1,当点D在线段BC上时,
①BC与CF的位置关系为: .
②BC,CD,CF之间的数量关系为: ;(将结论直接写在横线上)
(2)数学思考
如图2,当点D在线段CB的延长线上时,结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.
(3)拓展延伸
如图3,当点D在线段BC的延长线上时,延长BA交CF于点G,连接GE.若已知AB=2![]() ,CD=
,CD=![]() BC,请求出GE的长.
BC,请求出GE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线AB分别与x轴、y轴交于点B、C,与直线OA交于点A.已知点A的坐标为(﹣3,5),OC=4.
(1)分别求出直线AB、AO的解析式;
(2)求△ABO的面积.
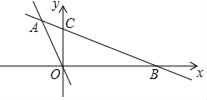
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com