
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,给出下列结论:①abc>0;②当x>2时,y>0;③3a+c>0;④3a+b>0.其中正确的结论有( ) 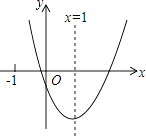
A.①②
B.①④
C.①③④
D.②③④
【答案】C
【解析】解:∵二次函数的图象的开口向上,
∴a>0,
∵二次函数的图象y轴的交点在y轴的负半轴上,
∴c<0,
∵二次函数图象的对称轴是直线x=1,
∴﹣ ![]() =1,
=1,
∴2a+b=0,b<0,
∴abc>0,∴①正确;
∵二次函数y=ax2+bx+c图象可知,当x>2时,y有小于0的情况,
∴②错误;
∵当x=﹣1时,y>0,
∴a﹣b+c>0,
把b=﹣2a代入得:3a+c>0,
∴③正确;
∵二次函数图象的对称轴是直线x=1,
∴﹣ ![]() =1,
=1,
∴2a+b=0,
∵a>0,
∴3a+b>0,故④正确.
故选C.
【考点精析】掌握二次函数图象以及系数a、b、c的关系和抛物线与坐标轴的交点是解答本题的根本,需要知道二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c);一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.


科目:初中数学 来源: 题型:
【题目】若a=0.32,b=﹣3﹣2,c=![]() ,d=
,d=![]() ,则它们的大小关系是( )
,则它们的大小关系是( )
A. a<b<c<d B. b<a<d<c C. a<d<c<b D. c<a<d<b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图的七边形ABCDEFG中,AB、ED的延长线相交于O点.若图中∠1、∠2、∠3、∠4的外角的角度和为220°,则∠BOD的度数是( )

A. 400 B. 450 C. 500 D. 600
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的三个顶点的坐标分别为A(﹣6,0)、B(﹣2,3)、
C(﹣1,0).
(1)请直接写出与点B关于坐标原点O的对称点B1的坐标;
(2)将△ABC绕坐标原点O逆时针旋转90°.画出对应的△A′B′C′图形,直接写出点A的对应点A′的坐标;
(3)若四边形A′B′C′D′为平行四边形,请直接写出第四个顶点D′的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=90°。

①当点D在AC上时,如图1,线段BD、CE有怎样的数量关系和位置关系?写出你猜想的结论,并说明理由;
②将图1中的△ADE绕点A顺时针旋转α角(0°<α<90°),如图2,线段BD、CE有怎样的数量关系和位置关系?请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=(x﹣1)2+n与x轴交于A,B两点(A在B的左侧),与y轴交于点C(0,﹣3),点D与点C关于抛物线的对称轴对称.
(1)求抛物线的解析式及点D的坐标;
(2)点P是抛物线对称轴上的一动点,当△PAC的周长最小时,求出点P的坐标;
(3)点Q在x轴上,且∠ADQ=∠DAC,请直接写出点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将长方形ABCD对折,得折痕PQ,展开后再沿MN翻折,使点C恰好落在折痕PQ上的点C′处,点D落在D′处,其中M是BC的中点且MN与折痕PQ交于F.连接AC′,BC′,则图中共有等腰三角形的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知 AB 是⊙O 的直径,点 C、D 在⊙O 上,过 D 点作 PF∥AC交⊙O 于 F,交 AB 于点 E,∠BPF=∠ADC
(1)求证:AEEB=DEEF.
(2)求证:BP 是⊙O 的切线:
(3)当的半径为![]() ,AC=2,BE=1 时,求 BP 的长,
,AC=2,BE=1 时,求 BP 的长,

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com