
【题目】如图,在平面直角坐标系中,直线y=![]() +n(n<0)与坐标轴交于A、B两点,与y=
+n(n<0)与坐标轴交于A、B两点,与y=![]() (x>0)交于点E,过点E作EF⊥x轴,垂足为F,且△OAB∽△FEB,相似比为
(x>0)交于点E,过点E作EF⊥x轴,垂足为F,且△OAB∽△FEB,相似比为![]() .
.
(1)若n=-![]() ,求m的值;
,求m的值;
(2)连接OE,试探究m与n的数量关系,并直接写出直线OE的解析式.

【答案】(1)m=3;(2)m=12n2, y=![]() x
x
【解析】
(1)利用直线方程求得A、B两点坐标,利用相似三角形的相似比求得点E的坐标,由待定系数法求得m的值;
(2)由函数图象上点的坐标特征探究m与n的数量关系,待定系数求得直线OE的解析式.
(1)当n=-![]() 时,直线方程是y=
时,直线方程是y=![]() ﹣
﹣![]() ,
,
当x=0时,y=﹣![]() ,即A(0,﹣
,即A(0,﹣![]() ),则OA=
),则OA=![]() ,
,
当y=0时,x=1,即B(1,0),则OB=1.
∵△OAB∽△FEB,相似比为![]() ,
,
∴EF=2OA=1,BF=2OB=2,
OF=OB+BF=1+2=3,
∴点E的坐标为(3,1),
∵点E在反比例函数y=![]() (x>0)的图象上,
(x>0)的图象上,
∴m=3×1=3;
(2)∵直线y=![]() +n(n<0)与坐标轴交于A、B两点,
+n(n<0)与坐标轴交于A、B两点,
∴当x=0时,y=n,即A(0,n),则OA=﹣n.
当y=0时,x=﹣2n,即B(﹣2n,0),则OB=﹣2n,
∵△OAB∽△FEB,相似比为![]() ,
,
∴EF=2OA=﹣2n,BF=2OB=﹣4n,
OF=OB+BF=﹣6n,
∴点E的坐标为(﹣6n,﹣2n).
∵点E在反比例函数y=![]() (x>0)的图象上,
(x>0)的图象上,
∴m=(﹣6n)(﹣2n)=12n2;
由点E的坐标为(﹣6n,﹣2n)得到直线OE的解析式为:y=![]() x.
x.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:
【题目】如图,为加快城乡对接,建设全域美丽乡村,某地区对A,B两地间的公路进行改建.如图,A,B两地之间有一座山,汽车原来从A地到B地需途径C地沿折线ACB行驶,现开通隧道后,汽车可直接沿直线AB行驶.已知BC=80千米,∠A=45°,∠B=30°,开通隧道后,汽车从A地到B地大约可以少走多少千米(结果精确到1千米)?(参考数据:![]() ≈1.4,
≈1.4,![]() ≈1.7)
≈1.7)

查看答案和解析>>
科目:初中数学 来源: 题型:
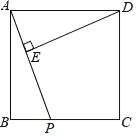
【题目】如图,在正方形ABCD中,AB=4,P是BC边上一动点(不与B,C重合),DE⊥AP于E.
(1)试说明△ADE∽△PAB;
(2)若PA=x,DE=y,请写出y与x之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D、E分别在边AB、AC上,DE∥BC,∠ACD=∠B,那么下列判断中,不正确的是( )
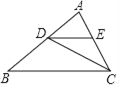
A. △ADE∽△ABC B. △CDE∽△BCD C. △ADE∽△ACD D. △ADE∽△DBC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为![]() ,连接AC、BD交于点O,CE平分∠ACD交BD于点E,
,连接AC、BD交于点O,CE平分∠ACD交BD于点E,
(1)求DE的长;
(2)过点EF作EF⊥CE,交AB于点F,求BF的长;
(3)过点E作EG⊥CE,交CD于点G,求DG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与双曲线
与双曲线![]() 交于点A.将直线
交于点A.将直线![]() 向右平移6个单位后,与双曲线
向右平移6个单位后,与双曲线![]() 交于点B,与x轴交于点C,若
交于点B,与x轴交于点C,若![]() ,则k的值为( )
,则k的值为( )
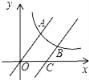
A. 12 B. 14 C. 18 D. 24
查看答案和解析>>
科目:初中数学 来源: 题型:
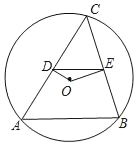
【题目】如图,在圆O中,弦AB=8,点C在圆O上(C与A,B不重合),连接CA、CB,过点O分别作OD⊥AC,OE⊥BC,垂足分别是点D、E.
(1)求线段DE的长;
(2)点O到AB的距离为3,求圆O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com