
【题目】如图,在圆O中,弦AB=8,点C在圆O上(C与A,B不重合),连接CA、CB,过点O分别作OD⊥AC,OE⊥BC,垂足分别是点D、E.
(1)求线段DE的长;
(2)点O到AB的距离为3,求圆O的半径.
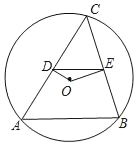
【答案】(1)DE=4;(2)圆O的半径为5.
【解析】
(1)根据垂径定理得出AD=DC,CE=EB,再根据三角形的中位线定理可得DE=![]() AB,代入相应数值求出即可;
AB,代入相应数值求出即可;
(2)过点O作OH⊥AB,垂足为点H,则OH=3,连接OA,根据垂径定理可得AH=4,在Rt△AHO中,利用勾股定理求出AO的长即可得答案.
(1)∵OD经过圆心O,OD⊥AC,
∴AD=DC,
同理:CE=EB,
∴DE是△ABC的中位线,
∴DE=![]() AB,
AB,
∵AB=8,
∴DE=4;
(2)过点O作OH⊥AB,垂足为点H,则OH=3,连接OA,

∵OH经过圆心O,
∴AH=BH=![]() AB,
AB,
∵AB=8,
∴AH=4,
在Rt△AHO中,AH2+OH2=AO2,
∴AO=5,即圆O的半径为5.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=![]() +n(n<0)与坐标轴交于A、B两点,与y=
+n(n<0)与坐标轴交于A、B两点,与y=![]() (x>0)交于点E,过点E作EF⊥x轴,垂足为F,且△OAB∽△FEB,相似比为
(x>0)交于点E,过点E作EF⊥x轴,垂足为F,且△OAB∽△FEB,相似比为![]() .
.
(1)若n=-![]() ,求m的值;
,求m的值;
(2)连接OE,试探究m与n的数量关系,并直接写出直线OE的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)一个不透明的口袋中装有2个红球(记为红球1、红球2)、1个白球、1个黑球,这些球除颜色外都相同,将球摇匀.
(1)从中任意摸出1个球,恰好摸到红球的概率是 ;
(2)先从中任意摸出1个球,再从余下的3个球中任意摸出1个球,请用列举法(画树状图或列表)求两次都摸到红球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,∠BAC=90°,AB=AC=2![]() ,D、E两点分别在AC、BC上,且DE∥AB,DC=2
,D、E两点分别在AC、BC上,且DE∥AB,DC=2![]() ,将△CDE绕点C顺时针旋转得到△CD′E′,如图2,点D、E对应点分别为D′、E′、D′、E′与AC相交于点M,当E′刚好落在边AB上时,△AMD′的面积为 .
,将△CDE绕点C顺时针旋转得到△CD′E′,如图2,点D、E对应点分别为D′、E′、D′、E′与AC相交于点M,当E′刚好落在边AB上时,△AMD′的面积为 .
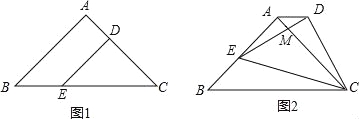
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某海域有两个海拔均为200米的海岛A和海岛B,一勘测飞机在距离海平面垂直高度为1100米的空中飞行,飞行到点C处时测得正前方一海岛顶端A的俯角是45°,然后沿平行于AB的方向水平飞行1.99×104米到达点D处,在D处测得正前方另一海岛顶端B的俯角是60°,求两海岛间的距离AB.
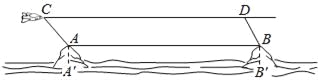
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AC切⊙O于点A,AD是⊙O的弦,OC⊥AD于F交⊙O于E,连接DE,BE,BD,AE.
(1)求证:∠C=∠BED;
(2)如果AB=10,tan∠BAD=![]() ,求AC的长;
,求AC的长;
(3)如果DE∥AB,AB=10,求四边形AEDB的面积.
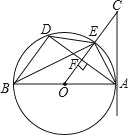
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知四边形ABCD为菱形,且A(0,4)、D(3,0).
(1)求经过点C的反比例函数的解析式;
(2)设P是(1)中所求函数图象上一点,以P、O、A顶点的三角形的面积与△COB的面积相等.求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com