
【题目】如图,四边形ABCD是菱形,∠B=60°,AB=1,扇形AEF的半径为1,圆心角为60°,则图中阴影部分的面积是_____.
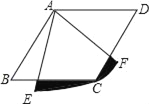
【答案】![]()
【解析】
根据菱形的性质得出△ADC和△ABC是等边三角形,进而利用全等三角形的判定得出△ADH≌△ACG,得出四边形AGCH的面积等于△ADC的面积,进而求出即可.
连接AC,
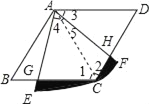
∵四边形ABCD是菱形,
∴∠B=∠D=60°,AB=AD=DC=BC=1,
∴∠BCD=∠DAB=120°,
∴∠1=∠2=60°,
∴△ABC、△ADC都是等边三角形,
∴AC=AD=1,
∵AB=1,
∴△ADC的高为![]() ,AC=1,
,AC=1,
∵扇形BEF的半径为1,圆心角为60°,
∴∠4+∠5=60°,∠3+∠5=60°,
∴∠3=∠4,
设AF、DC相交于HG,设BC、AE相交于点G,
在△ADH和△ACG中,
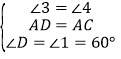 ,
,
∴△ADH≌△ACG(ASA),
∴四边形AGCH的面积等于△ADC的面积,
∴图中阴影部分的面积是:S扇形AEF﹣S△ACD=![]() =
=![]() ,
,
故答案为:![]() .
.


 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D、E分别在边AB、AC上,DE∥BC,∠ACD=∠B,那么下列判断中,不正确的是( )
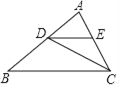
A. △ADE∽△ABC B. △CDE∽△BCD C. △ADE∽△ACD D. △ADE∽△DBC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,点E为AB边上的一点,点F为对角线BD上的一点,且EF⊥AB.若四边形ABCD为正方形.
①如图1,请直接写出AE与DF的数量关系 ;
②将△EBF绕点B逆时针旋转到图2所示的位置,连接AE,DF,猜想AE与DF的数量关系并说明理由.
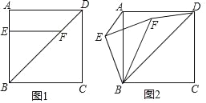
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,迎宾公园的喷水池边上有半圆形的石头(半径为1.12m)作为装饰,其中一块石头正前方5.88m处有一彩灯,某一时刻,该灯柱落在此半圆形石头上的影长为0.56πm.如果同一时刻,一直立0.6m的杆子的影长为1.8m,则灯柱的高____m.
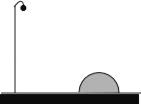
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A1的坐标为(2,0),过点A1作x轴的垂线交直线l:y=![]() x于点B1,以原点O为圆心,OB1的长为半径画弧交x轴正半轴于点A2;再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,以OB2的长为半径画弧交x轴正半轴于点A3;….按此作法进行下去,则
x于点B1,以原点O为圆心,OB1的长为半径画弧交x轴正半轴于点A2;再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,以OB2的长为半径画弧交x轴正半轴于点A3;….按此作法进行下去,则![]() 的长是_____.
的长是_____.
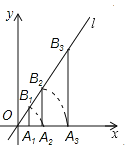
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在圆O中,弦AB=8,点C在圆O上(C与A,B不重合),连接CA、CB,过点O分别作OD⊥AC,OE⊥BC,垂足分别是点D、E.
(1)求线段DE的长;
(2)点O到AB的距离为3,求圆O的半径.
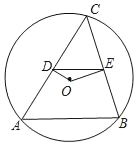
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是小李上学用的自行车,型号是24英吋(车轮的直径为24英吋,约60厘米),为了防止在下雨天骑车时的泥水溅到身上,他想在自行车两轮的阴影部分两侧装上挡水的铁皮(两个阴影部分分别是以C、D为圆心的两个扇形),量出四边形ABCD中∠DAB=125°、∠ABC=115°,那么预计需要的铁皮面积约是( )

A. 942平方厘米 B. 1884平方厘米
C. 3768平方厘米 D. 4000平方厘米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:抛物线y=x2+(2m﹣1)x+m2﹣1经过坐标原点,且当x<0时,y随x的增大而减小.
(1)求抛物线的解析式,并写出y<0时,对应x的取值范围;
(2)设点A是该抛物线上位于x轴下方的一个动点,过点A作x轴的平行线交抛物线于另一点D,再作AB⊥x轴于点B,DC⊥x轴于点C.
①当BC=1时,直接写出矩形ABCD的周长;
②设动点A的坐标为(a,b),将矩形ABCD的周长L表示为a的函数并写出自变量的取值范围,判断周长是否存在最大值?如果存在,求出这个最大值,并求出此时点A的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C都在抛物线y=ax2﹣2amx+am2+2m﹣5(其中﹣![]() <a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
<a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
(1)填空:抛物线的顶点坐标为 (用含m的代数式表示);
(2)求△ABC的面积(用含a的代数式表示);
(3)若△ABC的面积为2,当2m﹣5≤x≤2m﹣2时,y的最大值为2,求m的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com