
【题目】已知:抛物线y=x2+(2m﹣1)x+m2﹣1经过坐标原点,且当x<0时,y随x的增大而减小.
(1)求抛物线的解析式,并写出y<0时,对应x的取值范围;
(2)设点A是该抛物线上位于x轴下方的一个动点,过点A作x轴的平行线交抛物线于另一点D,再作AB⊥x轴于点B,DC⊥x轴于点C.
①当BC=1时,直接写出矩形ABCD的周长;
②设动点A的坐标为(a,b),将矩形ABCD的周长L表示为a的函数并写出自变量的取值范围,判断周长是否存在最大值?如果存在,求出这个最大值,并求出此时点A的坐标;如果不存在,请说明理由.
【答案】y=![]() -3x,0<x<3;6;
-3x,0<x<3;6;![]() ,(
,(![]() ,-
,-![]() )或(
)或(![]() ,-
,-![]() )
)
【解析】
试题(1)根据待定系数法,可得函数解析式,根据函数的增减性,可得符合条件的函数解析式,根据函数与不等式的关系,可得答案;
(2)①根据BC关于对称轴对称,可得A点的纵坐标,根据矩形的周长公式,可得答案;
②分类讨论A在对称轴左侧,A在对称轴右侧,根据对称,可得BC的长,AB的长,根据周长公式,可得函数解析式,根据函数的增减性,可得答案.
试题解析:(1)∵抛物线y=x2+(2m﹣1)x+m2﹣1经过坐标原点(0,0),
∴m2﹣1=0,
∴m=±1
∴y=x2+x或y=x2﹣3x,
∵当x<0时,y随x的增大而减小,
∴y=x2﹣3x,由函数与不等式的关系,得y<0时,0<x<3;
(2)①如图1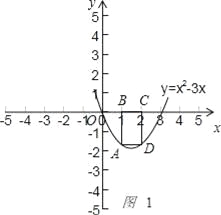 ,
,
当BC=1时,由抛物线的对称性,得点A的纵坐标为﹣2,
∴矩形的周长为6;
②∵A的坐标为(a,b),
∴当点A在对称轴左侧时,如图2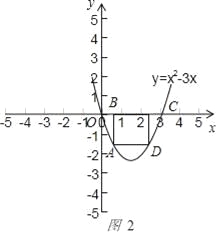 ,
,
矩形ABCD的一边BC=3﹣2a,另一边AB=3a﹣a2,
周长L=﹣2a2+2a+6.其中0<a<![]() ,当a=
,当a=![]() 时,L最大=
时,L最大=![]() ,A点坐标为(
,A点坐标为(![]() ,﹣
,﹣![]() ),
),
当点A在对称轴右侧时如图3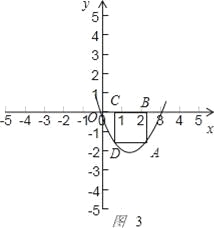 ,
,
矩形的一边BC=3﹣(6﹣2a)=2a﹣3,另一边AB=3a﹣a2,
周长L=﹣2a2+10a﹣6,其中![]() <a<3,当a=
<a<3,当a=![]() 时,L最大=
时,L最大=![]() ,A点坐标为(
,A点坐标为(![]() ,﹣
,﹣![]() );
);
综上所述:当0<a<![]() 时,L=﹣2(a﹣
时,L=﹣2(a﹣![]() )2+
)2+![]() ,
,
∴当a=![]() 时,L最大=
时,L最大=![]() ,A点坐标为(
,A点坐标为(![]() ,﹣
,﹣![]() ),
),
当![]() <a<3时,L=﹣2(a﹣
<a<3时,L=﹣2(a﹣![]() )2+
)2+![]() ,
,
∴当a=![]() 时,L最大=
时,L最大=![]() ,A点坐标为(
,A点坐标为(![]() ,﹣
,﹣![]() ).
).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
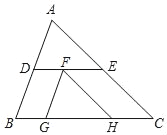
【题目】如图,在△ABC中,D、E分别是边AB、AC上的点,DE∥BC,点F在线段DE上,过点F作FG∥AB、FH∥AC分别交BC于点G、H,如果BG:GH:HC=2:4:3.求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把抛物线y=![]() x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=
x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=![]() x2交于点Q,则图中阴影部分的面积为 ▲ .
x2交于点Q,则图中阴影部分的面积为 ▲ .

查看答案和解析>>
科目:初中数学 来源: 题型:
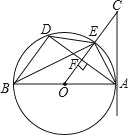
【题目】如图,AB是⊙O的直径,AC切⊙O于点A,AD是⊙O的弦,OC⊥AD于F交⊙O于E,连接DE,BE,BD,AE.
(1)求证:∠C=∠BED;
(2)如果AB=10,tan∠BAD=![]() ,求AC的长;
,求AC的长;
(3)如果DE∥AB,AB=10,求四边形AEDB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AC为直径的⊙O交与点M,交BC于点N,连接AN,过点C的切线交AB的延长线于点P.
(1)求证:∠BCP=∠BAN.
(2)若AC=4,PC=3,求MNBC的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
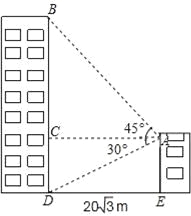
【题目】小敏家对面新建了一幢图书大厦,小敏在自家窗口测得大厦顶部的仰角为45°,大厦底部的仰角为30°,如图所示,量得两幢楼之间的距离为20![]() 米.
米.
(1)求出大厦的高度BD;
(2)求出小敏家的高度AE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形 ![]() 是菱形,
是菱形,![]() B=6,且∠ABC=60° ,M是菱形内任一点,连接AM,BM,CM,则AM+BM+CM 的最小值为________。
B=6,且∠ABC=60° ,M是菱形内任一点,连接AM,BM,CM,则AM+BM+CM 的最小值为________。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com