
| A. | y1<y2<y3 | B. | y2<y1<y3 | C. | y3<y1<y2 | D. | y3<y2<y1 |
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:解答题
| x(件) | … | 5 | 10 | 15 | 20 | … |
| y(元/件) | … | 75 | 70 | 65 | 60 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
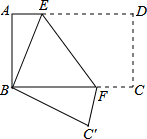 如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,若AB=1,BC=2,则△ABE和△BC′F的周长之和为( )
如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,若AB=1,BC=2,则△ABE和△BC′F的周长之和为( )| A. | 3 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
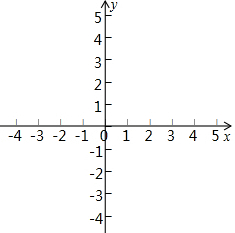 定义:对于平面直角坐标系xOy中的线段PQ和点M,在△MPQ中,当PQ边上的高为2时,称M为PQ的“等高点”,称此时MP+MQ为PQ的“等高距离”.
定义:对于平面直角坐标系xOy中的线段PQ和点M,在△MPQ中,当PQ边上的高为2时,称M为PQ的“等高点”,称此时MP+MQ为PQ的“等高距离”.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
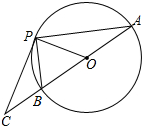 如图,AB为⊙O的直径,直线PC与⊙O相切于点P,交AB的延长线于C,∠PBC=120°,则∠PCB=( )
如图,AB为⊙O的直径,直线PC与⊙O相切于点P,交AB的延长线于C,∠PBC=120°,则∠PCB=( )| A. | 15° | B. | 30° | C. | 45° | D. | 60° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
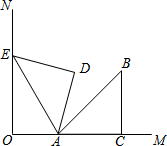 如图,ON⊥OM,等腰直角三角形ACB中,∠ACB=90°,边AC在OM上,将△ACB绕点A逆时针旋转75°,使得点B的对应点E恰好落在ON上,则$\frac{OA}{EA}$=$\frac{1}{2}$.
如图,ON⊥OM,等腰直角三角形ACB中,∠ACB=90°,边AC在OM上,将△ACB绕点A逆时针旋转75°,使得点B的对应点E恰好落在ON上,则$\frac{OA}{EA}$=$\frac{1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
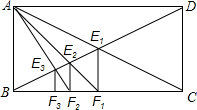 如图,矩形ABCD中,BC=1,连接AC与BD交于点E1,过E1作E1F1⊥BC于F1,连接AF1交BD于E2,过E2作E2F2⊥BC于F2,连接AF2交BD于E3,过E3作E3F3⊥BC于F3,…,以此类推,则BFn(其中n为正整数)的长为( )
如图,矩形ABCD中,BC=1,连接AC与BD交于点E1,过E1作E1F1⊥BC于F1,连接AF1交BD于E2,过E2作E2F2⊥BC于F2,连接AF2交BD于E3,过E3作E3F3⊥BC于F3,…,以此类推,则BFn(其中n为正整数)的长为( )| A. | $\frac{n}{n+1}$ | B. | $\frac{1}{n+1}$ | C. | $\frac{n+1}{n+2}$ | D. | $\frac{n+1}{n+3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com