
【题目】如图,在四边形ABCD 中,∠ABC=90°,AB=6,BC=8,CD=10,AD=10![]() ,
,
(1)求四边形ABCD的面积(2)求 BD的长
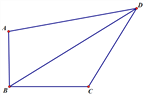
【答案】(1)74;(2)2![]()
【解析】(1)根据勾股定理的逆定理得出△ABC是直角三角形,进而求出四边形面积即可;
(2)过点D作DE⊥BC,交BC的延长线与点E,利用△ABC∽△CED求出BD的长即可.
(1)连接AC,
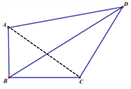
∵∠ABC=90°,
∴△ABC为直角三角形,AB=8,BC=6,∴AC=10,
又∵DA=10![]() ,CD=10,
,CD=10,
∴102+102=(10![]() )2
)2
AC2+CD2=DA2
所以△ACD为直角三角形.
四边形ABCD的面积S△ABC+S△ACD=![]() =74;
=74;
(2) 过点D作DE⊥BC,交BC的延长线与点E
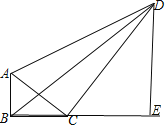
∵∠DEC=90°,∴∠DCE+∠CDE=90°,
所以∠DCE+∠ACB=90°,
∴∠CDE=∠ACB,又∵∠ABC=90°,
∴△ABC∽△CED
∴![]()
∴CE=6,DE=8.
∴BE=BC+CE=14,
在Rt△DEB中,
DB=![]() .
.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E是AB边的中点,F在AD边上,M,N分别是CD,BC边上的动点,若AB=AF=2,AD=3,则四边形EFMN周长的最小值是( ) 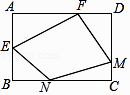
A.2+ ![]()
B.2 ![]() +2
+2 ![]()
C.5+ ![]()
D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习一元一次不等式与一次函数中,小明在同一个坐标系中分别做出了一次函数l1和l2的图像,l1与坐标轴的交点分别为点A、点B,l1与l2的交点为点C,但被同桌小英不小心用墨水给部分污染了,我们一起来探讨
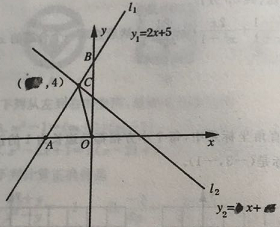
(1)写出点A、点C的坐标:A(①,0);C(②,4);
(2)求△BOC的面积:S△BOC=③
(3)直接写出不等式2x+5<·x+·的解集并回答下面问题
在解决问题(3)时,小明和小英各抒己见.小明:“l2的表达式中已经看不清楚了,并且只知道l2上一个点C的坐标,求不出该直线的表达式,所以无法求出该不等式的解集”小英说:“不用求出l2的表达式就可以得出该不等式的解集.”你同意谁的说法?并说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的对角线AC和BD交于点O,则下列不能判断四边形ABCD是平行四边形的条件是( )
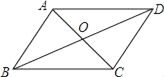
A. OA=OC,AD∥BC B. ∠ABC=∠ADC,AD∥BC
C. AB=DC,AD=BC D. ∠ABD=∠ADB,∠BAO=∠DCO
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,制作一种产品的同时,需要将原材料加热,设该材料温度为y℃,从加热开始计算的时间为x分钟,据了解,该材料在加热过程中温度y与时间x成一次函数关系,已知该材料在加热前的温度为15℃,加热5分钟使材料温度达到60℃时停止加热.停止加热后,材料温度逐渐下降,这时温度y与时间x成反比例函数关系. 
(1)分别求出该材料加热过程中和停止加热后y与x之间的函数表达式,并写出x的取值范围;
(2)根据工艺要求,在材料温度不低于30℃的这段时间内,需要对该材料进行特殊处理,那么对该材料进行特殊处理所用的时间是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:如图1,在平面内选一定点O,引一条有方向的射线Ox,再选定一个单位长度,那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定,有序数对(θ,m)称为M点的“极坐标”,这样建立的坐标系称为“极坐标系”. 应用:在图2的极坐标系下,如果正六边形的边长为2,有一边OA在射线Ox上,则正六边形的顶点C的极坐标应记为( )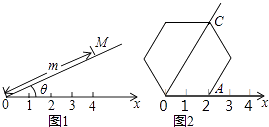
A.(60°,4)
B.(45°,4)
C.(60°,2 ![]() )
)
D.(50°,2 ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.则下列结论:①△ABG≌△AFG;②BG=CG;③AG∥CF;④S△EGC=S△AFE;⑤∠AGB+∠AED=145°.其中正确的个数是( )

A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com