
【题目】已知,平面直角坐标系中,A在x轴正半轴,B(0,1),∠OAB=30°.

(1)如图1,已知AB=2.点C在y轴的正半轴上,当△ABC为等腰三角形时,直接写出点C的坐标为 ;
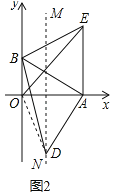
(2)如图2,以AB为边作等边△ABE,AD⊥AB交OA的垂直平分线于D,求证:BD=OE;
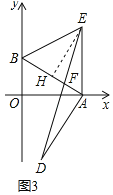
(3)如图3,在(2)的条件下,连接DE交AB于F,求![]() 的值.
的值.
【答案】(1)(0,3);(2)见解析;(3)![]()
【解析】
(1)由条件得出BC=AB=2, OC=OB+BC=3,从而可得到点C的坐标为(0,3);
(2)连接OD,证明△OAD是等边三角形,得出AO=AD,再证明△ABD≌△AEO(SAS),即可得出结论;
(3)作EH⊥AB于H,通过HL证明Rt△AEH≌Rt△BAO,得到EH=AO=AD,再通过AAS证明△HFE≌△AFD,得出EF=DF,即可求出![]() 的值.
的值.
(1)解:∵B(0,1),
∴OB=1,
∵AB=2,点C在y轴的正半轴上,△ABC为等腰三角形,
∴BC=AB=2,
∴OC=OB+BC=3,
∴点C的坐标为(0,3),
故答案为:(0,3);
(2)证明:连接OD,如图2所示:
∵△ABE是等边三角形,
∴AB=AE,∠BAE=60°,
∵∠OAB=30°,
∴∠OAE=30°+60°=90°,
∵AD⊥AB,
∴∠DAB=90°=∠OAE,∠OAD=90°﹣30°=60°,
∵MN是OA的垂直平分线,
∴OD=AD,
∴△OAD是等边三角形,
∴AO=AD,
在△ABD和△AEO中,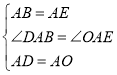 ,
,
∴△ABD≌△AEO(SAS),
∴BD=OE;
(3)解:作EH⊥AB于H,如图3所示:
∵△ABE是等边三角形,EH⊥AB,
∴AH=![]() AB,
AB,
∵∠AOB=90°,∠OAB=30°,
∴OB=![]() AB,
AB,
∴AH=OB,
在Rt△AEH和Rt△BAO中,![]() ,
,
∴△AEH≌△BAO(HL),
∴EH=AO=AD,
在△HFE和△AFD中,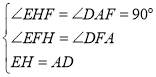 ,
,
∴△HFE≌△AFD(AAS),
∴EF=DF,
∴DE=2DF,
∴![]() =
=![]() .
.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:初中数学 来源: 题型:
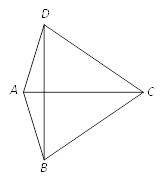
【题目】如图,在四边形ABCD中,AB=AD,AC是∠BAD的角平分线.
(1)求证:△ABC≌△ADC.
(2)若∠BCD=60°,AC=BC,求∠ADB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四幅图象分别表示变量之间的关系,请按图象的顺序,将下面的四种情境与之对应排序.正确的顺序是( )

①篮球运动员投篮时,投出去的篮球的高度与时间的关系
②去超市购买同一单价的水果,所付费用与水果数量的关系
③李老师使用的是一种含月租的手机计费方式,则他每月所付话费与通话时间的关系
④周末,小明从家到图书馆,看了一段时间书后,按原速度原路返回,小明离家的距离与时间的关系
A. ①②③④ B. ①③④② C. ①③②④ D. ①④②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M,N为圆心,大于![]() MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列结论中正确的个数是( )
MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列结论中正确的个数是( )
①AD是∠BAC的平分线;②∠ADC=60°;③AD=BD;④点D在AB的垂直平分线上⑤S△ABD=S△ACD

A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有![]() 、
、![]() 、
、![]() 三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )
三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )

A.在∠A、∠B两内角平分线的交点处
B.在AC、BC两边垂直平分线的交点处
C.在AC、BC两边高线的交点处
D.在AC、BC两边中线的交点处
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是一块锐角三角形材料,高线AH长8 cm,底边BC长10 cm,要把它加工成一个矩形零件,使矩形DEFG的一边EF在BC上,其余两个顶点D,G分别在AB,AC上,则四边形DEFG的最大面积为( )

A. 40 cm2 B. 20 cm2
C. 25 cm2 D. 10 cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
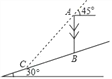
【题目】如图,在一个坡角为30°的斜坡上有一电线杆AB,当太阳光与水平线成45°角时,测得该杆在斜坡上的影长BC为20m.求电线杆AB的高(精确到0.1m,参考数值:![]() ≈1.73,
≈1.73,![]() ≈1.41).
≈1.41).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点![]() 经过某种变换后得到点
经过某种变换后得到点![]() ,我们把点
,我们把点![]()
![]() 叫做点
叫做点![]() 的终结点.已知点
的终结点.已知点![]() 的终结点为
的终结点为![]() ,点
,点![]() 的终结点为
的终结点为![]() ,点
,点![]() 的终结点为
的终结点为![]() ,这样依次得到
,这样依次得到![]() 、
、![]() 、
、![]() 、
、![]() …
…![]() ,若点
,若点![]() 的坐标为
的坐标为![]() ,则点
,则点![]() 的坐标为( )
的坐标为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com