Question

【题目】如图，在四边形ABCD中，AB=AD，AC是∠BAD的角平分线．

（1）求证：△ABC≌△ADC．

（2）若∠BCD＝60°，AC=BC，求∠ADB的度数．

Answer 1

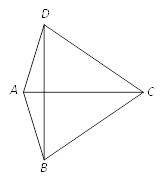
【答案】（1）详见解析；（2）∠ADB＝15°．

【解析】

（1）根据角平分线的性质可得∠DAC=∠BAC，从而利用SAS，可判定全等．

（2）根据△ABC≌△ADC．可知BC=DC，∠ACB＝∠ACD＝30°，已知∠BCD＝60°，故△BCD是等边三角形．即∠CBD＝60°，在△ABC中AC=BC，∠ACB＝30°，可得∠CDA＝75°，进而求得∠ADB＝15°．

解（1）∵AC是∠BAD的角平分线．

∴∠BAC=∠DAC，

∵AB=AD，AC=AC，

则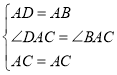

∴△ABC≌△ADC（SAS）．

（2）∵△ABC≌△ADC,∠BCD=60°,
∴∠DCA=∠BCA=30°，
∵AC=BC，
∴∠CAB=∠CAD=，
∵在△ADO与△ABO中

,

∴△ADO≌△ABO(SAS)，
∴∠AOD=∠AOB=90°，
∴∠ADB=90°75°=15°.