
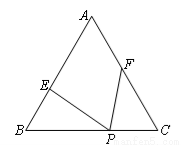
已知,等边△ABC边长为6,P为BC边上一点,且BP=4,点E、F分别在边AB、AC上,且∠EPF=60°,设BE=x,CF=y.
(1)求y与x的函数关系式,并写出x的取值范围;
(2)①若四边形AEPF的面积为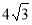 时,求x的值.
时,求x的值.
②四边形AEPF的面积是否存在最大值?若存在,请求出面积的最大值及此时x的值;若不存在,请说明理由.
(1) 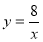 , x的取值范围是
, x的取值范围是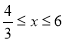 ;(2) ①4,②存在,x=2,
;(2) ①4,②存在,x=2,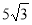 .
.
【解析】
试题分析:(1)求出△BEP∽△CPF,得出比例式,代入求出即可;
(2)①过A作AD⊥BC于D,过E作EN⊥BC于N,过F作FM⊥BC于M,求出AD=3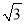 ,EN=
,EN=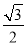 x,CF=y=
x,CF=y=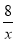 ,FM=
,FM=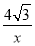 ,根据S四边形AEPF=S△ABC-S△BEP-S△CFP得出方程,求出x即可;
,根据S四边形AEPF=S△ABC-S△BEP-S△CFP得出方程,求出x即可;
②四边形AEPF的面积存在最大值,把9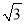 -
-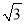 x-
x-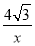 化成-
化成-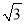 (
(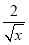 -
-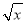 )2+5
)2+5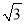 ,即可得出答案.
,即可得出答案.
试题解析:(1)∵∠EPF=60°
∴∠BPE+∠CPF=120°
∵∠B=60°∴∠BPE+∠BEP=120°
∴∠BEP=∠CPF又∵∠B=∠C=60°
∴△BEP∽△CPF
∴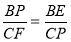
∴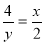
∴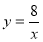 , x的取值范围是
, x的取值范围是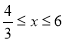 .
.
(2)①过A作AD⊥BC于D,
过E作EN⊥BC于N,过F作FM⊥BC于M
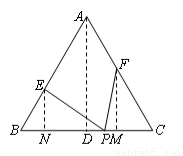
∵∠B=60°,AB=6,BE=x
∴AD=sin60°×6=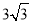 , EN=sin60°×x=
, EN=sin60°×x=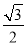 x
x
∵∠C=60°,CF=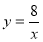 ∴FM=sin60°×
∴FM=sin60°×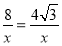
∴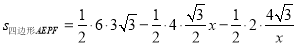
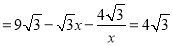 .
.
∴x2-5x+4=0
∴x1=1(舍去),x2=4
②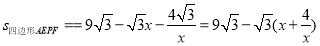
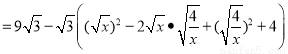
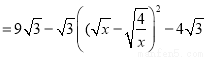
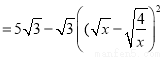
∴当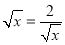 ,即x=2时,四边形AEPF的面积存在最大值,最大值是
,即x=2时,四边形AEPF的面积存在最大值,最大值是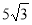 .
.
考点:1.相似三角形的判定与性质;2.一元二次方程的应用;3.二次函数的最值;4.等边三角形的性质.


科目:初中数学 来源:2013-2014学年江苏省无锡市崇安区九年级下学期期中统考(一模)数学试卷(解析版) 题型:填空题
如图所示,在△ABC中,∠B=90º,AB=3,AC=5,将△ABC折叠,使点C与点A重合,折痕为DE,则△ABE的周长为 .

查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省无锡市九年级3月阶段测试数学试卷(解析版) 题型:选择题
下列图形中,既是轴对称图形,又是中心对称图形的是( )

A. B. C. D.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省扬州市邗江区九年级中考一模数学试卷(解析版) 题型:解答题
小敏为了解本市的空气质量情况,从环境监测网随机抽取了若干天的空气质量情况作为样本进行统计,绘制了如图所示的条形统计图和扇形统计图(部分信息未给出).请你根据图中提供的信息,解答下列问题:

(1)计算被抽取的天数;
(2)请补全条形统计图,并求扇形统计图中表示优的扇形的圆心角度数;
(3)请估计该市这一年(365天)达到优和良的总天数.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省扬州市邗江区九年级中考一模数学试卷(解析版) 题型:填空题
用半径为10cm,圆心角为216°的扇形作一个圆锥的侧面,则这个圆锥的高是 cm.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省张家港市九年级5月网上阅卷适应性考试数学试卷(解析版) 题型:解答题
快、慢两车分别从相距360千米路程的甲、乙两地同时出发,匀速行驶,先相向而行,快车到达乙地后,停留1小时,然后按原路原速返回,快车比慢车晚1小时到达甲地,快、慢两车距各自出发地的路程y(千米)与出发后所用的时间x(小时)的关系如图所示.

请结合图象信息解答下列问题:
(1)慢车的速度是 千米/小时,快车的速度是 千米/小时;
(2)求m的值,并指出点C的实际意义是什么?
(3)在快车按原路原速返回的过程中,快、慢两车相距的路程为150千米时,慢车行驶了多少小时?
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省常州市九年级中考一模数学试卷(解析版) 题型:选择题
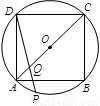
如图,正方形ABCD内接于⊙O,点P在劣弧AB上,连结DP,交AC于点Q.若QP=QO,则 的值为( )
的值为( )
A. B.
B.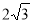 C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com