
【题目】如图,A、B两点分别位于一个池塘的两侧,池塘西边有一座假山D,在DB的中点C处有一个雕塑,小川从点A出发,沿直线AC一直向前经过点C走到点E,并使CE=CA,然后他测量点E到假山D的距离,则DE的长度就是A、B两点之间的距离.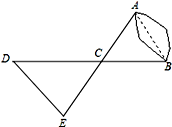
(1)你能说明小川这样做的根据吗?
(2)如果小川恰好未带测量工具,但是知道A和假山D、雕塑C分别相距200米、120米,你能帮助他确定AB的长度范围吗?
【答案】
(1)
解:∵C为BD中点.
∴BC=CD.
在△ABC和△EDC中.
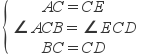
∴△ABC≌△EDC(SAS),
∴AB=DE;
(2)
解:∵AE-AD<DE<AD+AE,
又∵AC=CE=120,AB=DE,AD=200,
∴240-200<DE<200+240,
即40米<AB<440米
【解析】(1)由C为BD中点得BC=CD.又AC=CE,∠ACB=∠ECD,从而得△ABC≌△EDC(SAS),根据全等三角形的性质得出AB=DE;
(2)利用CE=CA,得出AE=240米,再利用DE=AB,在△ADE中根据三角形两边之和大于第三边,两边之差小于第三边即AE-AD<DE<AD+AE,从而可得出答案.
【考点精析】本题主要考查了三角形三边关系的相关知识点,需要掌握三角形两边之和大于第三边;三角形两边之差小于第三边;不符合定理的三条线段,不能组成三角形的三边才能正确解答此题.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:
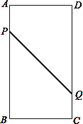
【题目】如图,在矩形ABCD中,AB=16cm,BC=6cm,点P从A出发沿AB以3cm/s的速度向点B移动,一直到达点B为止;同时,点Q从点C出发沿以2cm/s的速度向点D移动.经过多长时间P、Q两点的距离是10?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三角形的两边长分别为3和4,第三边长是方程x2﹣13x+40=0的根,则该三角形的周长是( )
A. 12B. 13C. 15D. 12或15
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,将点A(﹣1,1)向右平移2个单位长度得到点B,则点B关于x轴的对称点B的坐标为( )
A. (﹣3,﹣1)B. (1,﹣1)C. (﹣1,1)D. (﹣1,﹣3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com