【题目】如图，已知一次函数与反比例函数的图象相交于A（-4，-2），B(a，4)两点．
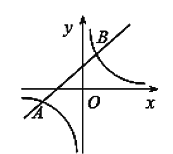
(1)求反比例函数的表达式和点B的坐标；
(2)根据图象直接同答：当白变量x在什么范围时，一次函数的值大于反比例函数的值．
【答案】（1）反比例函数的解析式是y=
，点B的坐标是（2,4）.（2）当x＞0或-4＜x＜0时，一次函数的值大于反比例函数的值.
【解析】
试题分析：（1）把点A坐标代到解析式中可求出反比例函数表达式，再把点B的坐标代入解析式可求出a的值（2）观察图像，一次函数图像在反比例函数图像上方的部分对应的x值即为所求，要注意自变量范围有两部分.
试题解析：（1）设反比例函数的解析式是y=
.∵点A（-4，-2）在此反比例函数图像上，∴
，∴k=8，∴反比例函数的解析式是y=.又∵点B（a，4）在此反比例函数图像上，∴
，a=2，点B的坐标是（2,4）.
（2）观察图像可知，当x＞0或-4＜x＜0时，一次函数的值大于反比例函数的值.
科目：初中数学 来源： 题型：
【题目】如图，已知，BC∥OA，∠B=∠A=100°，试回答下列问题：
（1）如图①，求证：OB∥AC．
（2）如图②，若点E、F在线段BC上，且满足∠FOC=∠AOC，并且OE平分∠BOF．求∠EOC的度数．
（3）在（2）的条件下，若平行移动AC，如图③，那么∠OCB：∠OFB的值是否随之发生变化？若变化，试说明理由；若不变，求出这个比值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】今年，我市全面启动“精准扶贫”工作，某校为了了解九年级贫困生人数，对该校九年级6个班进行摸排，得到各班贫困生人数分别为12，12，14，10，18，16，这组数据的众数和中位数分别是（ ）
A．12和10 B．12和13 C．12和12 D．12和14
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在△ABC中
，AO=BO，直线MN经过点O, 且AC⊥MN于C，BD⊥MN于D
(1) 当直线MN绕点O旋转到图①的位置时，求证：CD=AC+BD；
(2) 当直线MN绕点O旋转到图②的位置时，求证：CD=AC-BD；
(3) 当直线MN绕点O旋转到图③的位置时，试问：CD、AC、BD有怎样的等量关系？请写出这个等量关系，并加以证明。
查看答案和解析>>
科目：初中数学 来源： 题型：
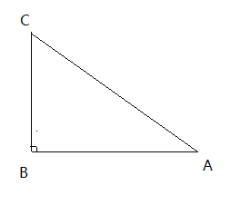
【题目】如图，已知△ABC中，∠B=90°，AB=8cm，BC=6cm。
（1）若P、Q是△ABC边上的两个动点，其中点P从A沿A→B方向运动，速度为每秒1cm，点Q从B沿B→C方向运动，速度为每秒2cm，两点同时出发，设出发时间为t秒．①当t=1秒时，求PQ的长；②从出发几秒钟后，△PQB是等腰三角形？
（2）若M在△ABC边上沿B→A→C方向以每秒3cm的速度运动，则当点M在边CA上运动时，求△BCM成为等腰三角形时M运动的时间．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，∠C=90°,AD是∠BAC的平分线，O是AB上一点,以OA为半径的⊙O经过点D。
（1）求证：BC是⊙O切线；
（2）若BD=5,DC=3,求AC的长。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
