
如图,平行四边形ABCD中,AB=3 cm,BC=5 cm,∠B=60°,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连接CE,DF.
(1)求证:四边形CEDF是平行四边形;
(2)①当AE= cm时,四边形CEDF是矩形;
②当AE= cm时,四边形CEDF是菱形.
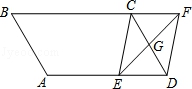
(1)证明:∵ 四边形ABCD是平行四边形,
∴ CF∥ED,∴ ∠FCG=∠EDG.
∵ G是CD的中点,∴CG=DG.
在△FCG和△EDG中,
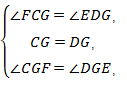
∴ △FCG≌△EDG(ASA),
∴ FG=EG.
∵ CG=DG,∴ 四边形CEDF是平行四边形;
(2)①解:当AE=3.5 cm时,平行四边形CEDF是矩形.
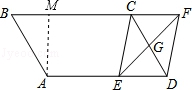 理由是:过A作AM⊥BC于M,
理由是:过A作AM⊥BC于M,
∵∠B=60°,AB=3,
∴BM=1.5 cm.
∵ 四边形ABCD是平行四边形,
 ∴ ∠CDA=∠B=60°,DC=AB=3 cm,BC=AD=5 cm.
∴ ∠CDA=∠B=60°,DC=AB=3 cm,BC=AD=5 cm.
∵ AE=3.5 cm,∴ DE=1.5 cm =BM.
在△MBA和△EDC中,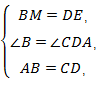
∴ △MBA≌△EDC(SAS),
∴ ∠CED=∠AMB=90°.
∵ 四边形CEDF是平行四边形,
∴ 四边形CEDF是矩形.
②当AE=2 cm时,四边形CEDF是菱形.
理由是:∵ AD=5 cm,AE=2 cm,∴ DE=3 cm.
∵ CD=3,∠CDE=60°,
∴ △CDE是等边三角形,∴ CE=DE.
∵ 四边形CEDF是平行四边形,
∴ 四边形CEDF是菱形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于( )
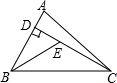
A.10 B.7 C.5 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
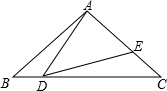
如图,在△ABC中,AB=AC=2,∠B=40°,点D在线段BC上运动(点D不与B、C两点重合),连接AD,作∠ADE=40°,连接AD,作∠ADE=40°,DE交线段AC于点E.
(1)当∠BDA=115°时,∠BAD=__________;点D从B向C运动时,∠BDA逐渐变__________(填“大”或“小”);
(2)当△ABD≌△DCE时,求CD的长;
(3)在点D的运动过程中,△ADE的形状也在改变,当∠BDA=110°时,请判断△ADE的形状,并证明之.
查看答案和解析>>
科目:初中数学 来源: 题型:
阅读下列解题过程:
已知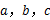 为△
为△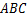 的三边长,且满足
的三边长,且满足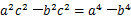 ,试判断△
,试判断△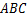 的形状.
的形状.
解:因为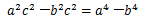 , ①
, ①
所以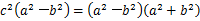 . ②
. ②
所以 . ③
. ③
所以△ 是直角三角形. ④
是直角三角形. ④
回答下列问题:
(1)上述解题过程,从哪一步开始出现错误?该步的序号为 .
(2)错误的原因为 .
(3)请你将正确的解答过程写下来.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com