
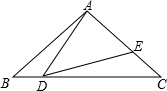
如图,在△ABC中,AB=AC=2,∠B=40°,点D在线段BC上运动(点D不与B、C两点重合),连接AD,作∠ADE=40°,连接AD,作∠ADE=40°,DE交线段AC于点E.
(1)当∠BDA=115°时,∠BAD=__________;点D从B向C运动时,∠BDA逐渐变__________(填“大”或“小”);
(2)当△ABD≌△DCE时,求CD的长;
(3)在点D的运动过程中,△ADE的形状也在改变,当∠BDA=110°时,请判断△ADE的形状,并证明之.
【考点】全等三角形的判定与性质;等腰三角形的性质.
【专题】动点型.
【分析】(1)利用邻补角的性质和三角形内角和定理解题;
(2)直接利用全等 三角形的对应边相等求解即可;
三角形的对应边相等求解即可;
(3)当∠BDA的度数为110°或80°时,△ADE的形状是等腰三角形.
【解答】解:(1)∠EDC=180°﹣∠ADB﹣∠ADE=180°﹣115°﹣40°=25°;
点D从B向C运动时,∠BDA逐渐变小;
(2)∵△ABD≌△DCE
∴AB=DC=2;
(3)当∠BDA的度数为110°时,△ADE的形状是等腰三角形,
证明:∵∠BDA=110°时,
∴∠ADC=70°,
∵∠C=40°,
∴∠DAC=70°,
∴∠ADC=∠DAC=70°,
∴△ADE的形状是等腰三角形.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:
已知如图,AC⊥BC,DE⊥AB,AD平分∠BAC,下面结论错误的是( )
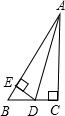
A.BD+ED=BC B.DE平分∠ADB C.AD平分∠EDC D.ED+AC>AD
查看答案和解析>>
科目:初中数学 来源: 题型:
(1)如图(1),将△ABC纸片沿着DE对折,使点A落在四边形BCDE内点A′的位置,探索∠A,∠1,∠2之间的数量关系,并说明理由.
(2)如图(2),继续这样的操作,把△ABC纸片的三个角按(1)的方式折叠,三个顶点都在形内,那么∠1+∠2+∠3+∠4+∠5+∠6的度数是__________.
(3)如果把n边形纸片也做类似的操作,n个顶点都在形内,那么∠1+∠2+∠3+…+∠2n的度数是______ ____ (用含有n的代数式表示).
____ (用含有n的代数式表示).
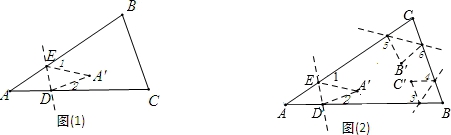
查看答案和解析>>
科目:初中数学 来源: 题型:
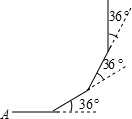
.如图,小亮从A点出发,沿直线前进10米后向左转36°,再沿直线前进10米,再向左转36°…照这样走下去,他第一次回到出发点A点时,一共走的路程是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,菱形ABCD中,AB=4,∠B=60°,AE⊥BC,AF⊥CD,垂足分別为E,F,连接EF,则△AEF的面积是( )
A.4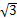 B.3
B.3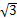 C.
C.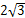 D.
D.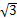

查看答案和解析>>
科目:初中数学 来源: 题型:
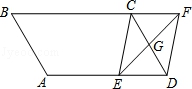
如图,平行四边形ABCD中,AB=3 cm,BC=5 cm,∠B=60°,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连接CE,DF.
(1)求证:四边形CEDF是平行四边形;
(2)①当AE= cm时,四边形CEDF是矩形;
②当AE= cm时,四边形CEDF是菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com