
(1)如图(1),将△ABC纸片沿着DE对折,使点A落在四边形BCDE内点A′的位置,探索∠A,∠1,∠2之间的数量关系,并说明理由.
(2)如图(2),继续这样的操作,把△ABC纸片的三个角按(1)的方式折叠,三个顶点都在形内,那么∠1+∠2+∠3+∠4+∠5+∠6的度数是__________.
(3)如果把n边形纸片也做类似的操作,n个顶点都在形内,那么∠1+∠2+∠3+…+∠2n的度数是______ ____ (用含有n的代数式表示).
____ (用含有n的代数式表示).
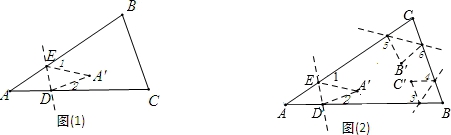
【考点】翻折变换(折叠问题).
【分析】(1)运用折叠原理及四边形的内角和定理即可解决问题;
(2)由折叠可知∠1+∠2+∠3+∠4+∠5+∠6=∠B+∠B'+∠C+∠C'+∠A+∠A',又知∠B=∠B',∠C=∠C',∠A=∠A',故能求出∠1+∠2+∠3+∠4+∠5+∠6的度数和;
(3)利用(1)(2)的计算方法:类比得出答案即可.
【解答】解:(1)连接AA′,
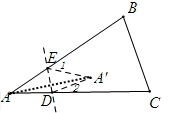
∵∠1=∠BAA′+∠AA′E,∠2=∠CAA′+∠AA′D,
∴∠1+∠2=∠BAA′+∠AA′E+∠CAA′+∠AA′D=∠BAC+∠DA′E,
又∵∠BAC=∠DA′E,
∴∠1+∠2=2∠BAC;
(2)∠1+∠2+∠3+∠4+∠5+∠6=∠B+∠B'+∠C+∠C'+∠A+∠A',
∵∠B=∠B',∠C=∠C',∠A=∠A',
∴∠1+∠2+∠3+∠4+∠5+∠6=2(∠B+∠C+∠A)=360°;
(3)∠1+∠2+∠3+…+∠2n
=2(∠B+∠C+∠A)(n﹣2)
=360°(n﹣2).
【点评】本题考查图形的折叠与拼接,同时考查了三角形、四边形等几何基本知识,掌握折叠的性质是解决问题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
点P(a﹣5,a﹣2)与点A(﹣4,a2)关于x轴对称,则P的坐标为( )
A.(﹣3,2) B.(﹣3,﹣2) C.(3,﹣2) D.(﹣4,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于( )
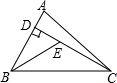
A.10 B.7 C.5 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
某同学把一块三角形的玻璃打碎成了3块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事方法是( )
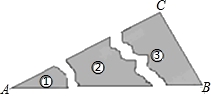
A.带①去 B.带②去 C.带③去 D.①②③都带去
查看答案和解析>>
科目:初中数学 来源: 题型:
已知下列语句:
(1)有两个锐角相等的直角三角形全等;
(2)斜边和一条直角边分别相等的两个直角三角形全等;
(3)三个角对应相等的两个三角形全等;
(4)两个直角三角形全等.
其中正确语句的个数为( )
A.0 B.1 C.2 D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在△ABC中,AB=AC=2,∠B=40°,点D在线段BC上运动(点D不与B、C两点重合),连接AD,作∠ADE=40°,连接AD,作∠ADE=40°,DE交线段AC于点E.
(1)当∠BDA=115°时,∠BAD=__________;点D从B向C运动时,∠BDA逐渐变__________(填“大”或“小”);
(2)当△ABD≌△DCE时,求CD的长;
(3)在点D的运动过程中,△ADE的形状也在改变,当∠BDA=110°时,请判断△ADE的形状,并证明之.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com