练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

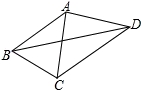
    如图，已知AB=AC=AD，∠CBD=2∠BDC，∠BAC=44°，则∠CAD的度数为__________．


    88°．

    【考点】圆周角定理．

    【分析】由AB=AC=AD，可得B，C，D在以A为圆心，AB为半径的圆上，然后由圆周角定理，证得∠CAD=2∠CBD，∠BAC=2∠BDC，继而可得∠CAD=2∠BAC．

    【解答】解：∵AB=AC=AD，

    ∴B，C，D在以A为圆心，AB为半径的圆上，

    ∴∠CAD=2∠CBD，∠BAC=2∠BDC，

    ∵∠CBD=2∠BDC，∠BAC=44°，

    ∴∠CAD=2∠BAC=88°．

    故答案为：88°．

    【点评】此题考查了圆周角定理．注意得到B，C，D在以A为圆心，AB为半径的圆上是解此题的关键．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


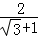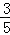
    在进行二次根式运算时，经常会遇到类似，的式子，其实我们还可以将其进一步变形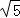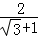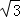：==；===﹣1．

    以上这种将分母变为有理式的恒等变形叫做分母有理化．

    再如：===﹣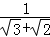

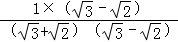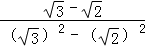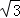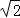
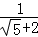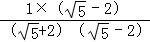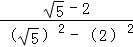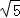    ===﹣2

    依照上述方法解答下列问题：

    （1）填空：=__________；=__________；=__________．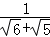

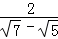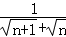    （2）化简求值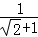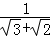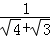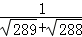：+++…+（写出解答过程）

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图所示，在∠AOB的两边截取AO=BO，CO=DO，连接AD、BC交于点P，考察下列结论，其中正确的是(     )

    ①△AOD≌△BOC；②△APC≌△BPD；③点P在∠AOB的平分线上．

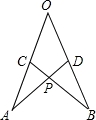
    A．只有①     B．只有②     C．只有①② D．①②③

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    一定能确定△ABC≌△DEF的条件是(     )

    A．∠A=∠D，AB=DE，∠B=∠E      B．∠A=∠E，AB=EF，∠B=∠D

    C．AB=DE，BC=EF，∠A=∠D  D．∠A=∠D，∠B=∠E，∠C=∠F

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在△ABC中，∠A：∠B：∠C=3：4：5，则∠C等于__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    （1）如图（1），将△ABC纸片沿着DE对折，使点A落在四边形BCDE内点A′的位置，探索∠A，∠1，∠2之间的数量关系，并说明理由．

    （2）如图（2），继续这样的操作，把△ABC纸片的三个角按（1）的方式折叠，三个顶点都在形内，那么∠1+∠2+∠3+∠4+∠5+∠6的度数是__________．

    （3）如果把n边形纸片也做类似的操作，n个顶点都在形内，那么∠1+∠2+∠3+…+∠2n的度数是__________  （用含有n的代数式表示）．

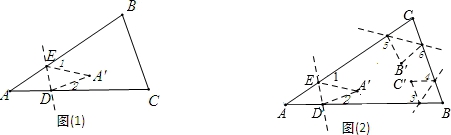
    查看答案和解析>>

    科目：初中数学 来源： 题型：


    现有3cm，4cm，7cm，9cm长的四根木棒，任取其中三根组成一个三角形，那么可以组成的三角形的个数是(     )

    A．1个  B．2个   C．3个  D．4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知：如图，C为BE上一点，点A，D分别在BE两侧，AB∥ED，AB=CE，BC=ED．求证：AC=CD．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若(2-a)x-4=5是关于x的一元一次方程，则a的取值范围是            。

    查看答案和解析>>

    同步练习册答案