
如图所示,在∠AOB的两边截取AO=BO,CO= DO,连接AD、BC交于点P,考察下列结论,其中正确的是( )
DO,连接AD、BC交于点P,考察下列结论,其中正确的是( )
①△AOD≌△BOC;②△APC≌△BPD;③点P在∠AOB的平分线上.
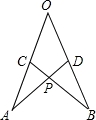
A.只有① B.只有② C.只有①② D.①②③
D【考点】全等三角形的判定与性质.
【分析】由AO=BO,∠O=∠O,DO=CO,①△AOD≌△BOC,∠A=∠B;
AO=BO,CO=DO⇒AC=BD,又∠A=∠B,∠APC=BPD⇒②△APC≌△BPD;
连接OP,容易证明△AOP≌△BOP⇒∠AOP=∠BOP⇒③点P在∠AOB的平分线上.
【解答】解:连接OP,
∵AO=BO,∠O=∠O,DO=CO,
∴△AOD≌△BOC,①正确;
∴∠A=∠B;
∵AO=BO,CO=DO,
∴AC=BD,又∠A=∠B,∠APC=BPD,
∴△APC≌△BPD,②正确;
∴AP=BP,
又AO=BO,OP=OP,
∴△AOP≌△BOP,
∴∠AOP=∠BOP,即点P在∠AOB的平分线上,③正确.
故选D.
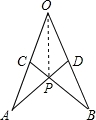
【点评】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、AAS、ASA和HL,做题时,要根据已知条件结合图形进行思考.


科目:初中数学 来源: 题型:
如图,在Rt△ABC中,在斜边AB和直角边AC上分别取一点D,E,使DE=DA,延长DE交BC的延长线于点F.△DFB是等腰三角形吗?请说明你的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
以下四种沿AB折叠的方法中,不一定能判定纸带两条边线a,b互相平行的是( )
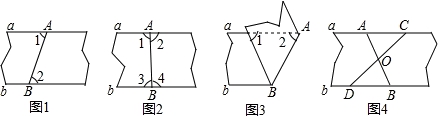
A.如图1,展开后测得∠1=∠2
B.如图2,展开后测得∠1=∠2且∠3=∠4
C.如图3,测得∠1=∠2
D.如图4,展开后再沿CD折叠,两条折痕的交点为O,测得OA=OB,OC=OD
查看答案和解析>>
科目:初中数学 来源: 题型:
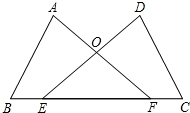
如图,点E、F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.
(1)求证:AB=DC;
(2)若∠EOF=60°试判断△OEF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
满足下列条件的三角形中,不是直角三角形的是( )
A.三内角之比为1∶2∶3 B.三边长的平方之比为1∶2∶3
C.三边长之比为3∶4∶5 D.三内角之比为3∶4∶5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com