
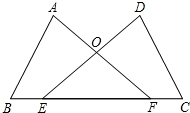
如图,点E、F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.
(1)求证:AB=DC;
(2)若∠EOF=60°试判断△OEF的形状,并说明理由.
【考点】全等三角形的判定与性质;等边三角形的判定与性质.
【分析】(1)易证BF=CE,即可求得△ABF≌△DCE,即可解题;
(2)根据(1)中求证的△ABF≌△DCE,即可求得∠OEF=∠OFE,即可解题.
【解答】解:(1)∵BE=CF,
∴BF=CE,
在△ABF和△DCE中,
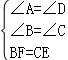 ,
,
∴△ABF≌△DCE,(AAS)
∴AB=DC;
(2)∵△AB F≌△DCE,
F≌△DCE,
∴∠OEF=∠OFE,
∵∠EOF=60°,
∴∠OEF=∠OFE=∠EOF=60°,
∴△OEF为等边三角形.
【点评】本题考查了全等三角形的判定,考查了全等三角形对应边、对应角相等的性质,考查了等边三角形的判定,本题中求证△ABF≌△DCE是解题的关键.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:
某校甲、乙两班参加植树活动,乙班先植树,然后甲班才开始与乙班一起植树.设甲班植树的总量为y甲(棵),乙班植树的总量为y乙(棵),两班一起植树所用的时间(从甲班开始植树时计时)为x(时),y甲、y乙分别与x之间的部分函数图象如图所示.下列说法正确的有( )
①甲班每小时植树20棵;
②乙班比甲班先植树30棵;
③甲班植树3小时两个班植树总量都是60棵;
④甲班植树超过3小时后,植树总量超过乙班.

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
如图①,已知等腰直角△ABC中,BD为斜边上的中线,E为DC上的一点,且AG⊥BE于G,AG交BD于F.
(1)求证:AF=BE;
(2)如图②,若点E在DC的延长线上,其它条件不变,①的结论还能成立吗?若不能,请说明理由;若能,请予以证明.

2015-2016学年山东省日照市五莲县八年级(上)期中数学试卷
查看答案和解析>>
科目:初中数学 来源: 题型:
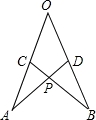
如图所示,在∠AOB的两边截取AO=BO,CO= DO,连接AD、BC交于点P,考察下列结论,其中正确的是( )
DO,连接AD、BC交于点P,考察下列结论,其中正确的是( )
①△AOD≌△BOC;②△APC≌△BPD;③点P在∠AOB的平分线上.
A.只有① B.只有② C.只有①② D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
一定能确定△ABC≌△DEF的条件是( )
A.∠A=∠D,AB=DE,∠B=∠E B.∠A=∠E,AB=EF,∠B=∠D
C.AB=DE,BC=EF,∠A=∠D D.∠A=∠D,∠B=∠E,∠C=∠F
查看答案和解析>>
科目:初中数学 来源: 题型:
现有3cm,4cm,7cm,9cm长的四根木棒,任取其中三根组成一个三角形,那么可以组成的三角形的个数是( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com