
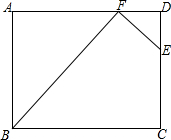
 如图,ABCD是长方形,AB=6,BC=8,CE=4,四边形BCEF的面积是30,那么三角形DEF的面积是多少?
如图,ABCD是长方形,AB=6,BC=8,CE=4,四边形BCEF的面积是30,那么三角形DEF的面积是多少? 科目:初中数学 来源: 题型:填空题
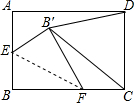 如图,在矩形ABCD中,AB=6,BC=8,点E为AB的中点,点F为BC边上任意一点,将△BEF沿EF翻折,点B的对应点为B′,则当△B′CD面积最小时折痕EF的长为3$\sqrt{2}$.
如图,在矩形ABCD中,AB=6,BC=8,点E为AB的中点,点F为BC边上任意一点,将△BEF沿EF翻折,点B的对应点为B′,则当△B′CD面积最小时折痕EF的长为3$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
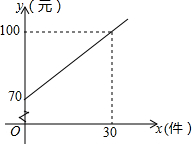 某快递公司的每位“快递小哥”日收入与每日的派送量成一次函数关系,如图所示.
某快递公司的每位“快递小哥”日收入与每日的派送量成一次函数关系,如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
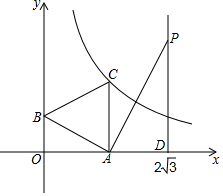 如图,一次函数y=-$\frac{{\sqrt{3}}}{3}$x+1的图象与x轴、y轴分别交于点A、B,以线段AB为边在第一象限作等边△ABC.
如图,一次函数y=-$\frac{{\sqrt{3}}}{3}$x+1的图象与x轴、y轴分别交于点A、B,以线段AB为边在第一象限作等边△ABC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,平面直角坐标系中,已知直线y=x上一点P(2,2)C为y轴上一点,连接PC,线段PC绕点P顺时针旋转90°至线段PD,过点D作直线AB⊥x轴,垂足为B,直线AB与直线y=x交于点A,且BD=2AD,连接CD,直线CD与直线y=x交于点Q.
如图,平面直角坐标系中,已知直线y=x上一点P(2,2)C为y轴上一点,连接PC,线段PC绕点P顺时针旋转90°至线段PD,过点D作直线AB⊥x轴,垂足为B,直线AB与直线y=x交于点A,且BD=2AD,连接CD,直线CD与直线y=x交于点Q.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
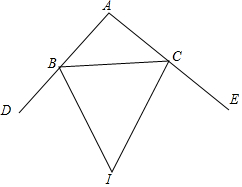 如图,BI,CI分别平分△ABC的外角∠DBC和∠ECB,
如图,BI,CI分别平分△ABC的外角∠DBC和∠ECB,查看答案和解析>>
科目:初中数学 来源: 题型:填空题
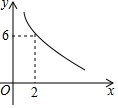 平行四边形ABCD中,AB⊥AC,∠B=45°.若平行四边形ABCD的一边长x与这条边上的高为y满足的反比例函数关系如图所示,则平行四边形ABCD的周长为4($\sqrt{3}$+$\sqrt{6}$).
平行四边形ABCD中,AB⊥AC,∠B=45°.若平行四边形ABCD的一边长x与这条边上的高为y满足的反比例函数关系如图所示,则平行四边形ABCD的周长为4($\sqrt{3}$+$\sqrt{6}$).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com