Question

19．如图，在等腰梯形ABCD中，AD∥BC，AB=CD，AD=6，BC=24，sinB=$\frac{4}{5}$，点P在边BC上，BP=8，点E在边AB上，点F在边CD上，且∠EPF=∠B，过点F作FG⊥PE交线段PE于点G，设BE=x，FG=y．
（1）求AB的长；
（2）当EP⊥BD时，求y的值；
（3）求y与x的函数关系式，并写出x的取值范围．

Answer 1

分析 （1）过点A作AP⊥BC交BC于点P，DF⊥BC交BC于点F，等腰梯形ABCD的性质，与sinB=$\frac{4}{5}$，求得AB即可；
（2）当EP⊥BC时，得出PF⊥CD，利用sinB=$\frac{4}{5}$，∠EPF=∠B=∠BCD，求得FG即可；
（3）过点E作EM⊥BC交BC于点M，利用勾股定理求得EP，进一步利用锐角三角函数的边关系得出答案即可．

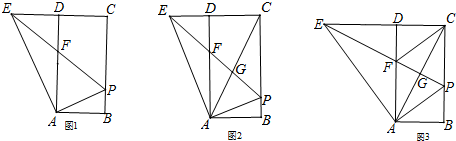
解答 解：（1）如图1，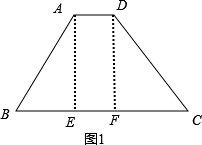

过点A作AP⊥BC交BC于点P，DF⊥BC交BC于点F，
∵AB=CD，AD=6，BC=24，
∴BE=（24-6）÷2=9，
∵sinB=$\frac{4}{5}$，
∴AB=9÷3×5=15；
（2）如图2，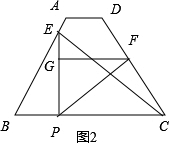

当EP⊥BC时，
△BEP，△FGP，△PCF都是直角三角形，
因此FG=FP•$\frac{4}{5}$=PC•$\frac{4}{5}$×$\frac{4}{5}$=（24-8）×$\frac{4}{5}$×$\frac{4}{5}$=$\frac{256}{25}$；
（3）如图3，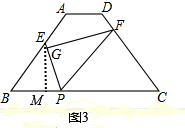

过点E作EM⊥BC交BC于点M，
则EP=$\sqrt{（8-\frac{3}{5}x）^{2}+（\frac{4}{5}x）^{2}}$，
PF=$\frac{16}{x}$•EP=$\frac{16}{x}$•$\sqrt{（8-\frac{3}{5}x）^{2}+（\frac{4}{5}x）^{2}}$，
y=$\frac{4}{5}$•$\frac{16}{x}$•$\sqrt{（8-\frac{3}{5}x）^{2}+（\frac{4}{5}x）^{2}}$
=$\frac{64}{5x}$•$\sqrt{\frac{9}{25}{x}^{2}-\frac{48}{5}x+64+\frac{16}{25}{x}^{2}}$
=$\frac{64\sqrt{25{x}^{2}-240x+1600}}{25x}$（$\frac{48}{5}$≤x≤15）

点评 此题考查等腰梯形的性质，锐角三角函数的意义，勾股定理，利用解决等腰梯形作辅助线的常用方法：作高解决问题，锐角函数建立直角三角形来解决问题．