Question

11．已知：如图1，矩形ABCD，P为BC上一动点，AE⊥AP交CD的延长线于E，EP交AD于F，AB=$\frac{1}{2}$BC，BC=nBP．
（1）求证：△ABP∽△ADE；
（2）连AC交PE于G，若n=4时，如图2，求$\frac{EF}{PG}$的值；
（3）连CF，如图3，当四边形APCF为菱形时，直接写出n的值为$\frac{8}{3}$．

Answer 1

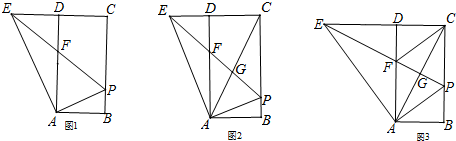
分析 （1）先证∠BAP=∠DAE，再由∠B=∠ADE=90°，根据三角形相似的判定方法即可得出结论；
（2）设BP=x，则BC=4x，CD=AB=$\frac{1}{2}$BC=2x，PC=3x，根据△ABP∽△ADE，得出比例式$\frac{DE}{AD}=\frac{BP}{AB}$，求出DE=2x，再根据勾股定理求出PE=5x，再由AD∥BC，得出△AGF∽△CGP，F为PE的中点，求出$\frac{FG}{PG}=\frac{AF}{PC}$=$\frac{5}{6}$，即可得出$\frac{EF}{PG}$的值；
（3）设BP=a，则BC=na，CD=AB=$\frac{na}{2}$；由△ABP∽△ADE，得出比例式求出DE=2a，再由四边形APCF为菱形，得出AC⊥PE，PE平分AC，证出AE=CE，再在Rt△ADE中，根据勾股定理得出AE²=AD²+DE²，即（na）²+（2a）²=$（2a+\frac{n}{2}a）^{2}$，即可求出n的值．

解答 （1）证明：∵四边形ABCD是矩形，
∴∠BAD=∠B=90°，AD=BC，AB=CD，
∴∠ADE=90°，
∵AE⊥AP，
∴∠PAE=90°，
∴∠BAP=∠DAE，∠B=∠ADE，
∴△ABP∽△ADE； 

（2）若n=4时，设BP=x，则BC=4x，CD=AB=$\frac{1}{2}$BC=2x，PC=3x，
∵△ABP∽△ADE，
∴$\frac{DE}{AD}=\frac{BP}{AB}$=$\frac{1}{2}$，
∴DE=2x，
∴DE=CD，CE=4x，
∴PE=$\sqrt{（3x）^{2}+（4x）^{2}}$=5x，
∵AD∥BC，
∴EF=PF=$\frac{5}{2}$x，△AGF∽△CGP，
∴F为PE的中点，AF=$\frac{1}{2}$PE=$\frac{5}{2}$x，$\frac{FG}{PG}=\frac{AF}{PC}$=$\frac{\frac{5}{2}x}{3x}$=$\frac{5}{6}$，
∴$\frac{PF}{PG}=\frac{11}{6}$，
∴$\frac{EF}{PG}$=$\frac{11}{6}$；

（3）设BP=a，则BC=na，CD=AB=$\frac{na}{2}$，
由（1）得：△ABP∽△ADE，
∴$\frac{DE}{AD}=\frac{BP}{AB}$，即$\frac{DE}{na}=\frac{a}{\frac{n}{2}a}$，
∴DE=2a，
∵四边形APCF为菱形，
∴AC⊥PE，PE平分AC，
∴AE=CE，
在Rt△ADE中，AE²=AD²+DE²，
∴（na）²+（2a）²=$（2a+\frac{n}{2}a）^{2}$，
解得：n=$\frac{8}{3}$；
故答案为：$\frac{8}{3}$．

点评 本题是相似形综合题，考查了相似三角形的判定与性质、勾股定理、菱形的性质，矩形的性质等知识，本题难度较大，综合性强，特别是（2）（3）中，通过设未知数，根据相似三角形的性质和勾股定理才能求解．