练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知抛物线与轴交于点，对称轴为．

    试用含的代数式表示、．

    当抛物线与直线交于点时，求此抛物线的解析式．

    求当取得最大值时的抛物线的顶点坐标．

    【答案】（1）；（2）抛物线为；（3）抛物线的顶点坐标为．

    【解析】

    （1）根据抛物线与y轴的交点可以得到c与a的关系，根据对称轴可以得到b与a的关系；
    （2）间已知点的坐标代入函数关系式并结合上题求得的系数的关系得到a、b、c的值即可求得其解析式；
    （3）b（c+6）=-2a（3a+6）=-6a2-12a=-6（a+1）2+6，从而确定a的值，确定二次函数的解析式后即可确定其顶点坐标．

    解：∵抛物线与轴交于点

    ∴

    ∵对称轴为，

    ∴

    ∴；

    ∵抛物线与直线交于点，

    ∴在抛物线上，

    ∴

    ∴

    ∴

    ∴抛物线为；∵

    当时，的最大值为；

    ∴抛物线

    故抛物线的顶点坐标为．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在等边三角形中，为边的中点，为边的延长线上一点，，于点.下列结论错误的是（ ）

    A.

    B.

    C.

    D..

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知关于的函数（为常数）

    （1）若函数的图象与轴恰有一个交点，求的值；

    （2）若函数的图象是抛物线，且顶点始终在轴上方，求的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】有一个边长为a的大正方形和四个边长为b的全等的小正方形（其中a>2b）,按如图方式摆放，并顺次连接四个小正方形落入大正方形内部的顶点，得到四边形ABCD.

    下面有四种说法：

    ①阴影部分周长为4a;

    ②阴影部分面积为（a+2b）（a-2b）;

    ③四边形ABCD周长为8a-4b;

    ④四边形ABCD的面积为a24ab4b2.

    所有合理说法的序号是____.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，点A，B的坐标分别为（1，0），（0，2），某抛物线的顶点坐标为D（－1，1）且经过点B，连接AB，直线AB与此抛物线的另一个交点为C，则S△BCD：S△ABO＝（ ）

    A. 8:1B. 6:1C. 5:1D. 4:1

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在等边三角形ABC的外侧作直线AP，点C关于直线AP的对称点为点D，连接AD，BD，其中BD交直线AP于点E.

    （1）依题意补全图形；（2）若∠PAC＝20°，求∠AEB的度数；

    （3）连结CE，写出AE, BE, CE之间的数量关系，并证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系xOy中，点A（0，8），点B（6，8）．

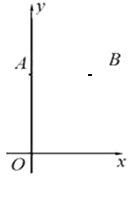
    （1）只用直尺（没有刻度）和圆规，求作一个点P，使点P同时满足下列两个条件：

    ①点P到A，B两点的距离相等； ②点P到∠xOy的两边的距离相等．（要求保留作图痕迹，不必写出作法）

    （2）在（1）作出点P后，点P的坐标为_________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某商店销售一款进价为每件40元的护肤品，调查发现，销售单价不低于40元且不高于80元时，该商品的日销售量y（件）与销售单价x（元）之间存在一次函数关系，当销售单价为44元时，日销售量为72件；当销售单价为48元时，日销售量为64件．

    （1）求y与x之间的函数关系式；

    （2）设该护肤品的日销售利润为w（元），当销售单价x为多少时，日销售利润w最大，最大日销售利润是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，P为△ABC内的一点，D，E，F分别是点P关于边AB，BC，CA所在直线的对称点，那么∠ADB+∠BEC+∠CFA=______°.

    查看答案和解析>>

    同步练习册答案