
【题目】已知![]() ,
,![]() ,
,![]() ,
,![]() (如图),点
(如图),点![]() ,
,![]() 分别为射线
分别为射线![]() 上的动点(点C、E都不与点B重合),连接AC、AE使得
上的动点(点C、E都不与点B重合),连接AC、AE使得![]() ,射线
,射线![]() 交射线
交射线![]() 于点
于点![]() ,设
,设![]() ,
,![]() .
.
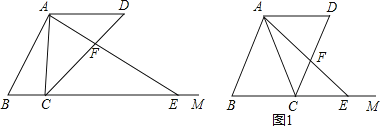
(1)如图1,当![]() 时,求AF的长.
时,求AF的长.
(2)当点![]() 在点
在点![]() 的右侧时,求
的右侧时,求![]() 关于
关于![]() 的函数关系式,并写出函数的定义域.
的函数关系式,并写出函数的定义域.
(3)连接![]() 交
交![]() 于点
于点![]() ,若
,若![]() 是等腰三角形,直接写出
是等腰三角形,直接写出![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]() 或
或![]() .
.
【解析】
过点![]() 作
作![]() 于N,利用∠B的余弦值可求出BN的长,利用勾股定理即可求出AN的长,根据线段的和差关系可得CN的长,利用勾股定理可求出AC的长,根据AD//BC,AD=BC即可证明四边形ABCD是平行四边形,可得∠B=∠D,进而可证明△ABC∽△ADF,根据相似三角形的性质即可求出AF的长;(2)根据平行线的性质可得
于N,利用∠B的余弦值可求出BN的长,利用勾股定理即可求出AN的长,根据线段的和差关系可得CN的长,利用勾股定理可求出AC的长,根据AD//BC,AD=BC即可证明四边形ABCD是平行四边形,可得∠B=∠D,进而可证明△ABC∽△ADF,根据相似三角形的性质即可求出AF的长;(2)根据平行线的性质可得![]() ,根据等量代换可得
,根据等量代换可得![]() ,进而可证明△ABC∽△ABE,根据相似三角形的性质可得
,进而可证明△ABC∽△ABE,根据相似三角形的性质可得![]() ,可用x表示出BE、CE的长,根据平行线分线段成比例定理可用x表示出
,可用x表示出BE、CE的长,根据平行线分线段成比例定理可用x表示出![]() 的值,根据
的值,根据![]() 可得y与x的关系式,根据x>0,CE>0即可确定x的取值范围;(3)分PA=PD、AP=AD和AD=PD三种情况,根据BE=
可得y与x的关系式,根据x>0,CE>0即可确定x的取值范围;(3)分PA=PD、AP=AD和AD=PD三种情况,根据BE=![]() 及线段的和差关系,分别利用勾股定理列方程求出x的值即可得答案.
及线段的和差关系,分别利用勾股定理列方程求出x的值即可得答案.
(1)如图,过点![]() 作
作![]() 于N,
于N,
∵AB=5,![]() ,
,
∴在![]() 中,
中,![]() =5×
=5×![]() =3,
=3,
∴AN=![]() =
=![]() =4,
=4,
∵BC=x=4,
∴CN=BC-BN=4-3=1,
在![]() 中,
中,![]() ,
,
∵AD=4,BC=x=4,
∴AD=BC,
∵![]() ,
,
∴四边形![]() 为平行四边形,
为平行四边形,
∴![]() ,
,
又∵![]() ,
,
∴△ABC∽△ADF,
∴![]() ,
,
∴![]()
解得:![]() ,
,
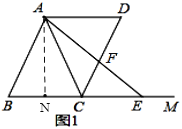
(2)∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
又∵∠B=∠B,
∴△ABC∽△ABE,
∴![]() ,
,
∴![]() ,
,
∵AD//BC,
∴![]() ,
,
∴![]() ,
,
∵x>0,CE=![]() >0,
>0,
∴0<x<5,
∴![]() ,
,
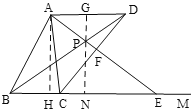
(3)①如图,当PA=PD时,作AH⊥BM于H,PG⊥AD于G,延长GP交BM于N,
∵PA=PD,AD=4,
∴AG=DG=2,∠ADB=∠DAE,
∵AD//BE,
∴GN⊥BE,∠DAE=∠AEB,∠ADB=∠DBE,
∴∠DBE=∠AEB,
∴PB=PE,
∴BN=EN=![]() BE=
BE=![]() ,
,
∵![]() ,AB=5,
,AB=5,
∴BH=AB·cos∠ABH=3,
∵AH⊥BM,GN⊥MB,GN⊥AD,
∴∠AHN=∠GNH=∠NGA=90°,
∴四边形AHNG是矩形,
∴HN=AG=2,
∴BN=BH+HN=3+2=5,
∴![]() =5,
=5,
解得:x=![]() .
.
②如图,当AP=AD=4时,作AH⊥BM于H,
∴∠ADB=∠APD,
∵AD//BM,
∴∠ADB=∠DBC,
∵∠APD=∠BPE,
∴∠DBC=∠BPE,
∴BE=PE=![]() ,
,
∵cos∠ABC=![]() ,AB=5,
,AB=5,
∴BH=3,AH=4,
∴在Rt△AEH中,(4+![]() )2=42+(3-
)2=42+(3-![]() )2,
)2,
解得:x=![]() ,
,
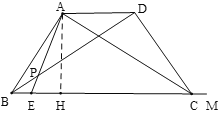
③如图,当AD=PD=4时,作AH⊥BM于H,DN⊥BM于N,
∴∠DAP=∠DPA,
∵AD//BM,
∴∠DAP=∠AEB,
∵∠APD=∠BPE,
∴∠BPE=∠AEB,
∴BP=BE=![]() ,
,
∵cos∠ABC=![]() ,AB=5,
,AB=5,
∴BH=3,AH=4,
∵AD//BM,AH⊥BM,DN⊥BM,
∴四边形AHND是矩形,
∴DN=AH=4,HN=AD=4,
中Rt△BND中,(4+![]() )2=42+(4+3)2,
)2=42+(4+3)2,
解得:x=![]() ,
,
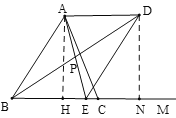
综上所述:x的值为![]() 或
或![]() 或
或![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边周长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x米.
(1)若苗圃园的面积为72平方米,求x;
(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由;
(3)当这个苗圃园的面积不小于100平方米时,直接写出x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有4个完全相同的小球,分别标有数字1、2、3、4,另有一个可以自由旋转的圆盘.被分成面积相等的3个扇形区,分别标有数字1、2、3(如图所示).小颖和小亮想通过游戏来决定谁代表学校参加歌咏比赛,游戏规则为:一人从口袋中摸出一个小球,另一个人转动圆盘,如果所摸球上的数字与圆盘上转出数字之和小于4,那么小颖去;否则小亮去.
(1)用树状图或列表法求出小颖参加比赛的概率;
(2)你认为该游戏公平吗?请说明理由;若不公平,请修改该游戏规则,使游戏公平.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是矩形ABCD内一点,连结P与矩形ABCD各顶点,矩形EFGH各顶点分别在边AP,BP,CP,DP上,已知AE=2EP,EF∥AB,图中两块阴影部分的面积和为S.则矩形ABCD的面积为( )
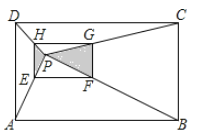
A.4SB.6SC.12SD.18S
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD中,AB=6,AD=8将矩形ABCD沿直线MN翻折后,点B恰好落在边AD上的点E处,如果AE=2AM,那么CN的长为______.
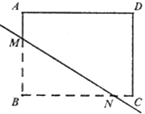
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“每天锻炼一小时,健康生活一辈子”.为了选拔“阳光大课间”领操员,学校组织初中三个年级推选出来的15名领操员进行比赛,成绩如下表:
成绩/分 | 7 | 8 | 9 | 10 |
人数/人 | 2 | 5 | 4 | 4 |
(1)这组数据的众数是多少,中位数是多少.
(2)已知获得2018年四川省南充市的选手中,七、八、九年级分别有1人、2人、1人,学校准备从中随机抽取两人领操,求恰好抽到八年级两名领操员的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的高,AE是BC边上的中线,∠C=45°,sinB=![]() ,AD=1.
,AD=1.
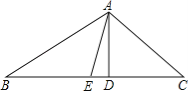
(1)求BC的长;
(2)求tan∠DAE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着阿里巴巴、淘宝网、京东、小米等互联网巨头的崛起,推动了快递行业的高速发展.据调查,岳阳市某家小型快递公司,今年1月份与3月份完成投递的快递总件数分别为8万件和9.68万件.现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递快递总件数的月平均增长率.
(2)如果平均每人每月可投递快递0.4万件,那么该公司现有的21名快递投递业务员能否完成今年4月份的快递投递任务?如果不能,请问至少需要增加几名业务员?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com