
【题目】图,已知:∠MON=30°,点A1、A2、A3在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A6B6A7的边长为 . 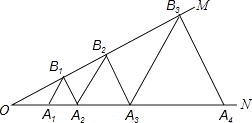
【答案】32
【解析】解:∵△A1B1A2是等边三角形,
∴A1B1=A2B1 , ∠3=∠4=∠12=60°,
∴∠2=120°,
∵∠MON=30°,
∴∠1=180°﹣120°﹣30°=30°,
又∵∠3=60°,
∴∠5=180°﹣60°﹣30°=90°,
∵∠MON=∠1=30°,
∴OA1=A1B1=1,
∴A2B1=1,
∵△A2B2A3、△A3B3A4是等边三角形,
∴∠11=∠10=60°,∠13=60°,
∵∠4=∠12=60°,
∴A1B1∥A2B2∥A3B3 , B1A2∥B2A3 ,
∴∠1=∠6=∠7=30°,∠5=∠8=90°,
∴A2B2=2B1A2 , B3A3=2B2A3 ,
∴A3B3=4B1A2=4,
A4B4=8B1A2=8,
A5B5=16B1A2=16,
以此类推:A6B6=32B1A2=32.
故答案是:32.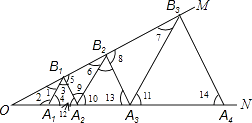
根据等腰三角形的性质以及平行线的性质得出A1B1∥A2B2∥A3B3 , 以及A2B2=2B1A2 , 得出A3B3=4B1A2=4,A4B4=8B1A2=8,A5B5=16B1A2…进而得出答案.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ACB中,∠ACB=90°,∠ABC=30°,AC=1,点D为AC上一动点,连接BD,以BD为边作等边△BDE,设CD=n. 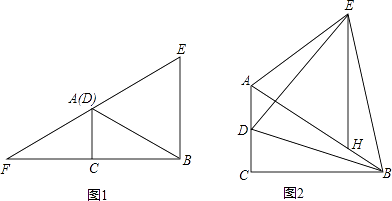
(1)当n=1时,EA的延长线交BC的延长线于F,则AF=;
(2)当0<n<1时,如图2,在BA上截取BH=AD,连接EH.
①设∠CBD=x,用含x的式子表示∠ADE和∠ABE.
②求证:△AEH为等边三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知2辆A型车和1辆B型车载满货物一次可运货10吨.用1辆A型车和2辆B型车载满货物一次可运货11吨.某物流公司现有31吨货物,计划同时租用A型车a辆和B型车b辆,一次运完,且每辆车都满载货物.根据以上信息解答下列问题:
(1)1辆A型车和1辆B型车载满货物一次分别可运货物多少吨?
(2)请帮助物流公司设计租车方案
(3)若A型车每辆车租金每次100元,B型车每辆车租金每次120元.请选出最省钱的租车方案,并求出最少的租车费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知线段AC∥y轴,点B在第一象限,且AO平分∠BAC,AB交y轴与G,连OB、OC. 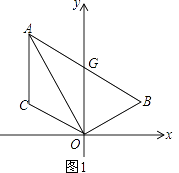
(1)判断△AOG的形状,并予以证明;
(2)若点B、C关于y轴对称,求证:AO⊥BO;
(3)在(2)的条件下,如图2,点M为OA上一点,且∠ACM=45°,BM交y轴于P,若点B的坐标为(3,1),求点M的坐标. 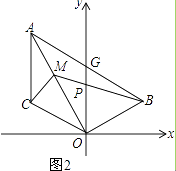
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作:
如图1,正方形ABCD中,AB=a,点E是CD边上一个动点,在AD上截取AG=DE,连接EG,过正方形的中线O作OF⊥EG交AD边于F,连接OE、OG、EF、AC.
探究:
在点E的运动过程中:
(1)猜想线段OE与OG的数量关系?并证明你的结论;
(2)∠EOF的度数会发生变化吗?若不会,求出其度数,若会,请说明理由.
应用:
(3)当a=6时,试求出△DEF的周长,并写出DE的取值范围;
(4)当a的值不确定时:
①若![]() =
=![]() 时,试求
时,试求![]() 的值;
的值;
②在图1中,过点E作EH⊥AB于H,过点F作FG⊥CB于G,EH与FG相交于点M;并将图1简化得到图2,记矩形MHBG的面积为S,试用含a的代数式表示出S的值,并说明理由.
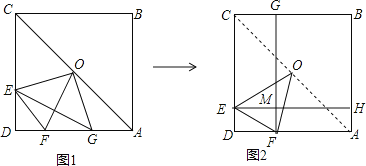
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场去年前五个月销售额共计![]() 万元.下表表示该商场去年前五个月的月销售额(统计信息不全).图①表示该商场服装部各月销售额占商场当月销售额的百分比情况统计图.
万元.下表表示该商场去年前五个月的月销售额(统计信息不全).图①表示该商场服装部各月销售额占商场当月销售额的百分比情况统计图.
商场月销售额统计表
单位:万元
月份 |
|
|
|
|
|
商场月销售额 |
|
|
|
|
服装部各月销售额占市场 当月销售额的百分比统计图 |
占 |
|
|
(![]() )商场
)商场![]() 月份的销售额是__________万元.
月份的销售额是__________万元.
(![]() )服装部
)服装部![]() 月份的销售额是__________万元.
月份的销售额是__________万元.
小明同学观察图①后认为,服装部![]() 月份的销售额比服装部
月份的销售额比服装部![]() 月份的销售额减少了,你同意他的看法吗?请说明理由.
月份的销售额减少了,你同意他的看法吗?请说明理由.
答:__________.
(![]() )在该商场服装部,下设
)在该商场服装部,下设![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 五个卖区,图②表示在
五个卖区,图②表示在![]() 月份,服装部各卖区销售额占
月份,服装部各卖区销售额占![]() 月份服装部销售额的百分比情况统计图.则__________卖区的销售额最高,销售额最高的卖区占
月份服装部销售额的百分比情况统计图.则__________卖区的销售额最高,销售额最高的卖区占![]() 月份商场销售额的百分比是__________.
月份商场销售额的百分比是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列四个结论,①过三点可以作一个圆;②圆内接四边形对角相等;③平分弦的直径垂直于弦;④相等的圆周角所对的弧也相等;不正确的是( )
A.②③B.①③④C.①②④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果三条线段的长a,b,c满足a2=c2-b2,则这三条线段组成的三角形是( )
A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 无法确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com