
【题目】如图1,已知线段AC∥y轴,点B在第一象限,且AO平分∠BAC,AB交y轴与G,连OB、OC. 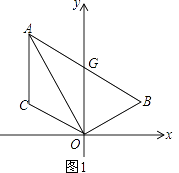
(1)判断△AOG的形状,并予以证明;
(2)若点B、C关于y轴对称,求证:AO⊥BO;
(3)在(2)的条件下,如图2,点M为OA上一点,且∠ACM=45°,BM交y轴于P,若点B的坐标为(3,1),求点M的坐标. 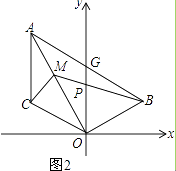
【答案】
(1)解:△AOG的形状是等腰三角形,
理由如下:
∵AC∥y轴,
∴∠CAO=∠GOA,
∵AO平分∠BAC,
∴∠CAO=∠GAO,
∴∠GOA=∠GAO,
∴AG=OG,
∴△AOG是等腰三角形
(2)解:如图1,接连BC,过O作OE⊥AB于E,过点C作CD⊥x轴于点D,
∵B、C关于y轴对称,AC∥y轴,
∴AC⊥BC,
在Rt△COD和Rt△BOE中,
![]() ,
,
∴△COD≌△BOE(HL),
∴∠DCO=∠EBO,
∴∠BAC+∠BOC=180°,
设∠BAO=∠CAO=x,∠OBC=∠OCB=y,
∴2x+∠BOC=180°,
又∵2y+∠BOC=180°,
∴x=y,故∠OAC=∠OBC,
∴∠AOB=∠ACB=90°,
∴AO⊥OB
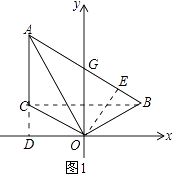
(3)解:如图2,连BC,作MF⊥x轴于F,BH⊥x轴于H,
则∠ACB=90°,
∵∠ACM=45°,
∴CM平分∠ACB,又AM平分∠BAC,
∴BM平分∠ABC,设∠ABM=∠CBM=z,
由(2)可得∠OMB=x+z,∠OBM=y+z=x+z
∴∠OMB=∠OBM,
∴OM=OB
∴△OBM为等腰直角三角形,
∵ 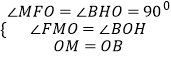 ,
,
∴△OMF≌△OBH(AAS),
∴OF=BH=1,MF=OH=3,
∴M(﹣1,3)
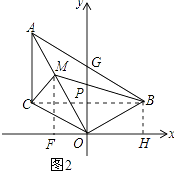
【解析】(1)△AOG的形状是等腰三角形,利用已知条件证明AG=OG即可;(2)接连BC,易证△COD≌△BOE(HL),设∠BAO=∠CAO=x,∠OBC=∠OCB=y,利用全等三角形的性质和已知条件证明∠AOB=∠ACB=90°,即可得到AO⊥BO;(3)连BC,作MF⊥x轴于F,BH⊥x轴于H,易证△OMF≌△OBH,OF=BH=1,MF=OH=3,所以M(﹣1,3).


科目:初中数学 来源: 题型:
【题目】对于命题“已知:a∥b,b∥c,求证:a∥c”.如果用反证法,应先假设( )
A. a不平行b B. b不平行c C. a⊥c D. a不平行c
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料并填空:
在平面直角坐标系![]() 中,点
中,点![]() 经过变换
经过变换![]() 得到点
得到点![]() ,变换记作
,变换记作![]() ,其中
,其中![]() (
(![]() ,
, ![]() 为常数).例如,当
为常数).例如,当![]() ,且
,且![]() 时,
时, ![]() .
.
(![]() )当
)当![]() ,且
,且![]() 时,
时, ![]() __________.
__________.
(![]() )若
)若![]() ,则
,则![]() __________,
__________, ![]() __________.
__________.
(![]() )设点
)设点![]() 的坐标满足
的坐标满足![]() ,点
,点![]() 经过变换
经过变换![]() 得到点
得到点![]() ,若点
,若点![]() 到点
到点![]() 重合,求
重合,求![]() 和
和![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)(﹣10)+(+7)
(2)12﹣(﹣18)+(﹣7)﹣15
(3)5.6+(﹣0. 9)+4.4+(﹣8.1)+(﹣0.1)
(4)|﹣22+(﹣3)2|﹣(﹣![]() )3
)3
(5)2×(﹣3)2﹣33﹣6÷(﹣2)
(6)﹣81÷![]() ×(﹣
×(﹣![]() )
)
(7)![]() +(﹣
+(﹣![]() )﹣(﹣
)﹣(﹣![]() )+(﹣
)+(﹣![]() )﹣(+
)﹣(+![]() )
)
(8)(﹣1)2008+(﹣5)×[(﹣2)3+2]﹣(﹣4)2÷(﹣![]() )
)
(9)﹣32×(﹣![]() )2+(
)2+(![]() ﹣
﹣![]() +
+![]() )×(﹣24).
)×(﹣24).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图,已知:∠MON=30°,点A1、A2、A3在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A6B6A7的边长为 . 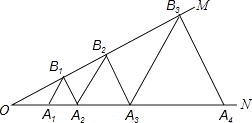
查看答案和解析>>
科目:初中数学 来源: 题型:
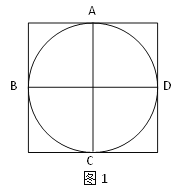
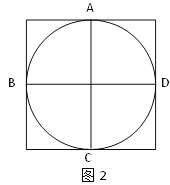
【题目】在图1、图2中,⊙O经过了正方形网格中的格点A、B、C、D,现请你仅用无刻度的直尺分别在图1、图2中画出一个满足下列条件的∠P:
(1)顶点P在⊙O上且不能与点A、B、C、D重合;
(2)∠P在图1、图2中的正切值分别为1、![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com