
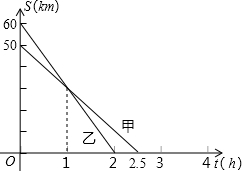
 已知A、B、C三地在同一条笔直的公路上,甲、乙两人骑自行车分别从B、C两地前往A地.他们距A地的路程S(km)与行驶时间t(h)之间的关系如图所示,请根据图象所提供的信息解答下列问题:
已知A、B、C三地在同一条笔直的公路上,甲、乙两人骑自行车分别从B、C两地前往A地.他们距A地的路程S(km)与行驶时间t(h)之间的关系如图所示,请根据图象所提供的信息解答下列问题:分析 (1)由函数图象得出对应的路程、时间,根据速度=路程÷时间进行解答即可;
(2)分两种情况讨论,即可解答;
(3)根据函数图象,即可解答.
解答 解:(1)由函数图象可得:B与A之间的距离为50km,C与A之间的距离为60km,甲从B到A所用的时间为2.5h,乙从C到A所用的时间为2h,
甲的速度为:50÷2.5=20(km/h),
乙的速度:60÷2=30(km/h).
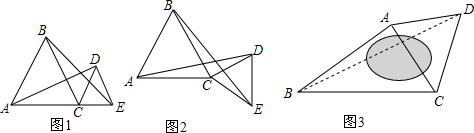
(2)①如图1,
当行驶一小时后甲乙两人相遇,两人相距0km;
②如图2,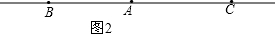
当行驶一小时后甲乙两人相遇,两人相距:50+60-20-30=60(km);
(3)由函数图象可得,当1<t<2.5时,乙比甲距离A地更近.
点评 本题考查了一次函数的应用,解决本题的关键是读懂函数图象,获取相关信息.


 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
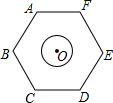 如图,圆心O恰好为正六边形ABCDEF的中心,已知AB=2$\sqrt{3}$,⊙O的半径为1,现将⊙O在正六边形内部沿某一方向平移,当它与正六边形ABCDEF的某条边相切时停止平移,设此时平移的距离为d,则d的取值范围是2≤d≤$\frac{4\sqrt{3}}{3}$.
如图,圆心O恰好为正六边形ABCDEF的中心,已知AB=2$\sqrt{3}$,⊙O的半径为1,现将⊙O在正六边形内部沿某一方向平移,当它与正六边形ABCDEF的某条边相切时停止平移,设此时平移的距离为d,则d的取值范围是2≤d≤$\frac{4\sqrt{3}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
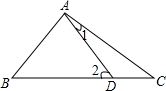 如图,已知D是BC上一点,且满足AB=AC=BD,那么∠1与∠2的关系是( )
如图,已知D是BC上一点,且满足AB=AC=BD,那么∠1与∠2的关系是( )| A. | 3∠2-∠1=180° | B. | ∠1+2∠2=180° | C. | 2∠1+∠2=180° | D. | ∠1=2∠2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com