
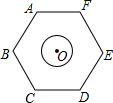
 如图,圆心O恰好为正六边形ABCDEF的中心,已知AB=2$\sqrt{3}$,⊙O的半径为1,现将⊙O在正六边形内部沿某一方向平移,当它与正六边形ABCDEF的某条边相切时停止平移,设此时平移的距离为d,则d的取值范围是2≤d≤$\frac{4\sqrt{3}}{3}$.
如图,圆心O恰好为正六边形ABCDEF的中心,已知AB=2$\sqrt{3}$,⊙O的半径为1,现将⊙O在正六边形内部沿某一方向平移,当它与正六边形ABCDEF的某条边相切时停止平移,设此时平移的距离为d,则d的取值范围是2≤d≤$\frac{4\sqrt{3}}{3}$. 分析 当圆O运动到圆P处时,运动距离最短,当圆O运动到圆Q处时,运动距离最长,分别求得PO和OQ的长即可得出d的取值范围.
解答 解:连接OB、OE,如图所示: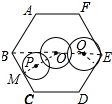
根据题意得:OB=OE=AB=2$\sqrt{3}$,
当圆O运动到圆P处时,运动距离最短,
由正六边形的性质得:
PO=OM-PM=OB•sin60°-1=3-1=2,;
当圆O运动到与DE、EF相切时,运动距离最长,
由正六边形的性质得:
OQ=OE-QE=2$\sqrt{3}$-$\frac{1}{cos60°}$=2$\sqrt{3}$-$\frac{2\sqrt{3}}{3}$=$\frac{4\sqrt{3}}{3}$;
∴2≤d≤$\frac{4\sqrt{3}}{3}$.
故答案为:2≤d≤$\frac{4\sqrt{3}}{3}$.
点评 本题主要考查的是正六边形的性质和直线和圆的位置关系,利用正六边形的性质、直线和圆相切,确定出平移后圆心的位置是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 在Rt△ABC中,∠C=90°,若tanA=$\frac{3}{4}$,则a=3,b=4 | |
| B. | 若△ABC三边之比为1:$\sqrt{3}$:$\sqrt{2}$,且∠A为最小角,则sinA=$\frac{1}{2}$ | |
| C. | 对于锐角α,必有sinα>cosα | |
| D. | 在Rt△ABC中,若∠C=90°,则sin2A+cos2A=1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
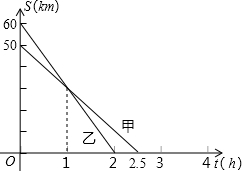 已知A、B、C三地在同一条笔直的公路上,甲、乙两人骑自行车分别从B、C两地前往A地.他们距A地的路程S(km)与行驶时间t(h)之间的关系如图所示,请根据图象所提供的信息解答下列问题:
已知A、B、C三地在同一条笔直的公路上,甲、乙两人骑自行车分别从B、C两地前往A地.他们距A地的路程S(km)与行驶时间t(h)之间的关系如图所示,请根据图象所提供的信息解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
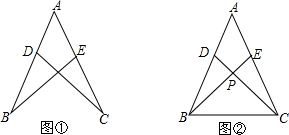
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
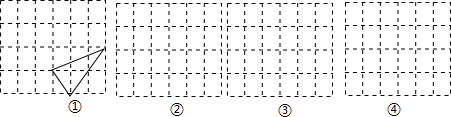
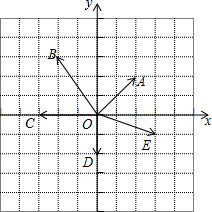 如图,在单位正方形网格中,建立直角坐标系,设$\overrightarrow{i}$、$\overrightarrow{j}$分别是x轴、y轴上的单位向量,试用$\overrightarrow{i}$、$\overrightarrow{j}$的线性组合表示下列在图中标出的向量.(直接将结果填在横线上)
如图,在单位正方形网格中,建立直角坐标系,设$\overrightarrow{i}$、$\overrightarrow{j}$分别是x轴、y轴上的单位向量,试用$\overrightarrow{i}$、$\overrightarrow{j}$的线性组合表示下列在图中标出的向量.(直接将结果填在横线上) 查看答案和解析>>
科目:初中数学 来源: 题型:解答题
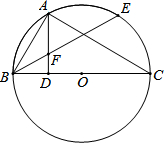 如图,BC是⊙O的直径,A是⊙O上一点,AD⊥BC,垂足为D,$\widehat{AE}$=$\widehat{AB}$,BE交AD于点F.
如图,BC是⊙O的直径,A是⊙O上一点,AD⊥BC,垂足为D,$\widehat{AE}$=$\widehat{AB}$,BE交AD于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com