
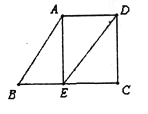
【题目】如图,已知AB∥DE,∠B=60°,AE⊥BC,垂足为点E.
(1)求∠AED的度数;
(2)当∠EDC满足什么条件时,AE∥DC,证明你的结论.
【答案】(1)30°;(2)当∠EDC=30°时, AE∥DC,理由参见解析.
【解析】试题分析:(1)由已知AE⊥BC,可知∠AEC=90°,根据AB∥DE,∠B=60°,得出∠DEC=∠B= 60°(两直线平行,同位角相等),这样∠AED就求出来了;(2)此题是平行线的判定,上题已求出∠AED=30°,利用内错角相等,两直线平行,只要∠EDC=30°就可以判定AE∥DC.
试题解析:(1)∵ AB∥DE, ∴ ∠DEC=∠B= 60°(两直线平行,同位角相等),又∵ BC⊥AE,∴ ∠AEC=90°(垂直定义),所以 ∠AED=90°-60°=30°; (2)由⑴得∠AED=30°,根据内错角相等,两直线平行,∴ ∠AED=∠EDC时 AE∥DC,即当∠EDC=30°时, AE∥DC.


科目:初中数学 来源: 题型:
【题目】某校八年级数学实践能力考试选择项目中,选择数据收集项目和数据分析项目的学生比较多。为了解学生数据收集和数据分析的水平情况,进行了抽样调查,过程如下,请补充完整.收集数据:从选择数据收集和数据分析的学生中各随机抽取16人,进行了体育测试,测试成绩(十分制)如下:
数据收集 | 10 | 9.5 | 9.5 | 10 | 8 | 9 | 9.5 | 9 | 7 | 10 | 4 | 5.5 | 10 | 7.9 | 9.5 | 10 |
数据分析 | 9.5 | 9 | 8.5 | 8.5 | 10 | 9.5 | 10 | 8 | 6 | 9.5 | 10 | 9.5 | 9 | 8.5 | 9.5 | 6 |
整理,描述数据:按如下分数段整理,描述这两组样本数据:
|
|
|
| 10 | |
数据收集 | 1 | 1 | 3 | 6 | 5 |
数据分析 |
(说明:成绩8.5分及以上为优秀,6分及以上为合格,6分以下为不合格.)
分析数据:两组样本数据的平均数,中位数,众数如下表所示:
项目 | 平均数 | 中位数 | 众数 |
数据收集 | 8.75 | 9.5 | 10 |
数据分析 | 8.81 | 9.25 | 9.5 |
得出结论:
(1)如果全校有480人选择数据收集项目,达到优秀的人数约为________人;
(2)初二年级的井航和凯舟看到上面数据后,井航说:数据分析项目整体水平较高.凯舟说:数据收集项目整体水平较高.你同意________的看法,理由为_______________________.(至少从两个不同的角度说明推断的合理性)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1, 在![]() 中,
中,![]() ,
,![]() .点O是BC的中点,点D沿B→A→C方向从B运动到C.设点D经过的路径长为
.点O是BC的中点,点D沿B→A→C方向从B运动到C.设点D经过的路径长为![]() ,图1中某条线段的长为y,若表示y与x的函数关系的图象大致如图2所示,则这条线段可能是图1中的 ( )
,图1中某条线段的长为y,若表示y与x的函数关系的图象大致如图2所示,则这条线段可能是图1中的 ( )
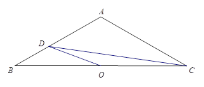
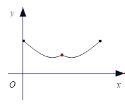
图1 图2
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)实施新课程改革后,学生的自主学习、合作交流能力有很大提高,张老师为了了解所教班级学生自主学习、合作交流的具体情况,对本班部分学生进行了为期三个月的跟踪调查,并将调查结果分成四类,A:特别好;B:好;C:一般;D:较差;并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:

(1)本次调查中,张老师一共调查了 名同学,其中C类女生有 名,D类男生有 名;
(2)将上面的条形统计图补充完整;
(3)为了共同进步,张老师想从被调查的A类和D类学生中分别选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
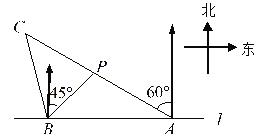
【题目】如图,在一笔直的海岸线![]() 上有
上有![]() 、
、![]() 两个观测站,
两个观测站,![]() 在
在![]() 的正东方向,
的正东方向,![]() (单位:
(单位:![]() )有一艘小船在点
)有一艘小船在点![]() 处,从
处,从![]() 测得小船在北偏西
测得小船在北偏西![]() 的方向,从
的方向,从![]() 测得小船在北偏东
测得小船在北偏东![]() 的方向.(结果保留根号)
的方向.(结果保留根号)
(1)求点![]() 到海岸线
到海岸线![]() 的距离;
的距离;
(2)小船从点![]() 处沿射线
处沿射线![]() 的方向航行一段时间后,到达点
的方向航行一段时间后,到达点![]() 处,此时,从
处,此时,从![]() 测得小船在北偏西
测得小船在北偏西![]() 的方向,求点
的方向,求点![]() 与点
与点![]() 之间的距离.
之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
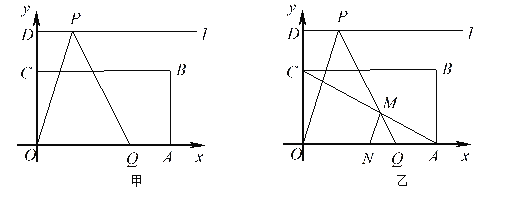
【题目】如图(13),矩形![]() 中,
中,![]() 、
、![]() 、
、![]() ,射线
,射线![]() 过点
过点![]() 且与
且与![]() 轴平行,点
轴平行,点![]() 、
、![]() 分别是
分别是![]() 和
和![]() 轴正半轴上动点,满足
轴正半轴上动点,满足![]() .
.
(1)①点![]() 的坐标是 ;②
的坐标是 ;②![]() = 度;③当点
= 度;③当点![]() 与点
与点![]() 重合时,点
重合时,点![]() 的坐标为 ;
的坐标为 ;
(2)设![]() 的中点为
的中点为![]() ,
,![]() 与线段
与线段![]() 相交于点
相交于点![]() ,连结
,连结![]() ,如图(13)乙所示,若
,如图(13)乙所示,若![]() 为等腰三角形,求点
为等腰三角形,求点![]() 的横坐标;
的横坐标;
(3)设点![]() 的横坐标为
的横坐标为![]() ,且
,且![]() ,
,![]() 与矩形
与矩形![]() 的重叠部分的面积为
的重叠部分的面积为![]() ,试求
,试求![]() 与
与![]() 的函数关系式.
的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
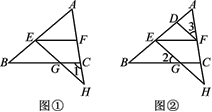
【题目】如图①,在三角形ABC中,点E,F分别为线段AB,AC上任意两点,EG交BC于点G,交AC的延长线于点H,∠1+∠AFE=180°.
(1)证明:BC∥EF;
(2)如图②,若∠2=∠3,∠BEG=∠EDF,证明:DF平分∠AFE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
(问题情境)
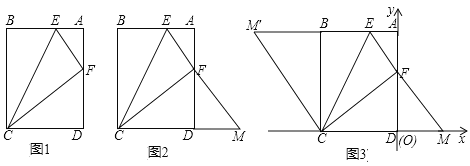
在综合与实践课上,同学们以“矩形的折叠”为主题展开数学活动,如图1,在矩形纸片ABCD中,AB=4,BC=5,点E,F分别为边AB,AD上的点,且DF=3。
(操作发现)
(1)沿CE折叠纸片,B点恰好与F点重合,求AE的长;
(2)如图2,延长EF交CD的延长线于点M,请判断△CEM的形状,并说明理由。
(深入思考)
(3)把图2置于平面直角坐标系中,如图3,使D点与原点O重合,C点在x轴的负半轴上,将△CEM沿CE翻折,使点M落在点M′处.连接CM′,求点M′的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,点A,B,C是数轴上的三个点,其中AB=12,且A,B两点表示的数互为相反数.
![]()
(1)请在数轴上标出原点O,并写出点A表示的数;
(2)如果点Q以每秒2个单位的速度从点B出发向左运动,那么经过 秒时,点C恰好是BQ的中点;
(3)如果点P以每秒1个单位的速度从点A出发向右运动,那么经过多少秒时PC=2PB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com