
【题目】某校八年级数学实践能力考试选择项目中,选择数据收集项目和数据分析项目的学生比较多。为了解学生数据收集和数据分析的水平情况,进行了抽样调查,过程如下,请补充完整.收集数据:从选择数据收集和数据分析的学生中各随机抽取16人,进行了体育测试,测试成绩(十分制)如下:
数据收集 | 10 | 9.5 | 9.5 | 10 | 8 | 9 | 9.5 | 9 | 7 | 10 | 4 | 5.5 | 10 | 7.9 | 9.5 | 10 |
数据分析 | 9.5 | 9 | 8.5 | 8.5 | 10 | 9.5 | 10 | 8 | 6 | 9.5 | 10 | 9.5 | 9 | 8.5 | 9.5 | 6 |
整理,描述数据:按如下分数段整理,描述这两组样本数据:
|
|
|
| 10 | |
数据收集 | 1 | 1 | 3 | 6 | 5 |
数据分析 |
(说明:成绩8.5分及以上为优秀,6分及以上为合格,6分以下为不合格.)
分析数据:两组样本数据的平均数,中位数,众数如下表所示:
项目 | 平均数 | 中位数 | 众数 |
数据收集 | 8.75 | 9.5 | 10 |
数据分析 | 8.81 | 9.25 | 9.5 |
得出结论:
(1)如果全校有480人选择数据收集项目,达到优秀的人数约为________人;
(2)初二年级的井航和凯舟看到上面数据后,井航说:数据分析项目整体水平较高.凯舟说:数据收集项目整体水平较高.你同意________的看法,理由为_______________________.(至少从两个不同的角度说明推断的合理性)
科目:初中数学 来源: 题型:
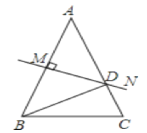
【题目】已知:如图,AB=AC,∠A=36°,AB的垂直平分线交AC于D,则下列结论:①∠C=72°;②BD是∠ABC的平分线;③△ABD是等腰三角形;④△BCD是等腰三角形,其中正确的有____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从泰州乘“K”字头列车A、“T”字头列车B都可直达南京,已知A车的平均速度为80 km/h,B车的平均速度为A车的1.5倍,且行完全程B车所需时间比A车少40分钟.
(1)求泰州至南京的铁路里程;
(2)若两车以各自的平均速度分别从泰州、南京同时相向而行,问经过多少时间两车相距40 km?
查看答案和解析>>
科目:初中数学 来源: 题型:
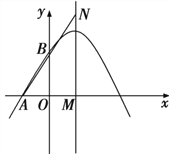
【题目】如图,抛物线![]() 过
过![]() 两点.
两点.
![]() 求抛物线的解析式.
求抛物线的解析式.
![]() 为抛物线对称轴与x轴的交点,N为对称轴上一点,若
为抛物线对称轴与x轴的交点,N为对称轴上一点,若![]() ,求M到AN的距离.
,求M到AN的距离.
![]() 在抛物线的对称轴上是否存在点P,使
在抛物线的对称轴上是否存在点P,使![]() 为等腰三角形?若存在,请直接写出满足条件的点
为等腰三角形?若存在,请直接写出满足条件的点
P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
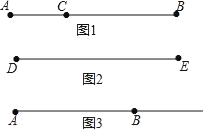
【题目】定义:若线段上的一个点把这条线段分成1:2的两条线段,则称这个点是这条线段的三等分点.如图1,点C在线段AB上,且AC:CB=1:2,则点C是线段AB的一个三等分点,显然,一条线段的三等分点有两个.
(1)已知:如图2,DE=15cm,点P是DE的三等分点,求DP的长.
(2)已知,线段AB=15cm,如图3,点P从点A出发以每秒1cm的速度在射线AB上向点B方向运动;点Q从点B出发,先向点A方向运动,当与点P重合后立马改变方向与点P同向而行且速度始终为每秒2cm,设运动时间为t秒.
①若点P点Q同时出发,且当点P与点Q重合时,求t的值.
②若点P点Q同时出发,且当点P是线段AQ的三等分点时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠ABC的平分线交AC于点E,过点E作BE的垂线交AB于点F,⊙O是△BEF的外接圆.
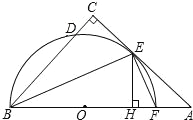
(1)求证:AC是⊙O的切线.
(2)过点E作EH⊥AB于点H,求证:CD=HF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于(﹣1)n= ,所以我们通常把(﹣1)n称为符号系数.
,所以我们通常把(﹣1)n称为符号系数.
(1)观察下列单项式:﹣![]() ,…按此规律,第5个单项式是 ,第n个单项式是 .
,…按此规律,第5个单项式是 ,第n个单项式是 .
(2)![]() 的值为 ;
的值为 ;
(3)你根据(2)写出一个当n为偶数时值为2,当n为奇数时值为0的式子 .
查看答案和解析>>
科目:初中数学 来源: 题型:
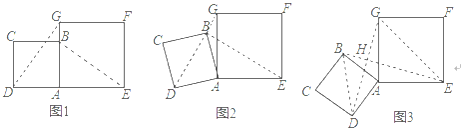
【题目】在数学兴趣小组活动中,小明将边长为2的正方形![]() 与边长为
与边长为![]() 的正方形
的正方形![]() 按如图1方式放置,
按如图1方式放置,![]() 与
与![]() 在同一条直线上,
在同一条直线上,![]() 与
与![]() 在同一条直线上.
在同一条直线上.
(1)请你猜想![]() 与
与![]() 之间的数量与位置关系,并加以证明;
之间的数量与位置关系,并加以证明;
(2)在图2中,若将正方形![]() 绕点
绕点![]() 逆时针旋转,当点
逆时针旋转,当点![]() 恰好落在线段
恰好落在线段![]() 上时,求出
上时,求出![]() 的长;
的长;
(3)在图3中,若将正方形![]() 绕点
绕点![]() 继续逆时针旋转,且线段
继续逆时针旋转,且线段![]() 与线段
与线段![]() 相交于点
相交于点![]() ,写出
,写出![]() 与
与![]() 面积之和的最大值,并简要说明理由.
面积之和的最大值,并简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
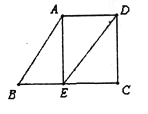
【题目】如图,已知AB∥DE,∠B=60°,AE⊥BC,垂足为点E.
(1)求∠AED的度数;
(2)当∠EDC满足什么条件时,AE∥DC,证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com